The Definition of Individual Biological Fitness

“Fitness” is one of the central concepts in biology. Despite this, the concept is still not clearly defined. Previous attempts at definition refer to what should be called an individual’s “potential fitness,” or, when mathematized, the relative fitness of genetic alleles. In contrast, the present work defines the actual fitness of an individual, exactly what is referred to in the expression “survival of the fittest.” This represents a new conceptualization, a mathematical definition that will extend across the entire set of ideas related to evolution.

In 1869, in the fifth edition of “On the Origin of Species,” Darwin [1] endorsed the formulation ‘survival of the fittest,’ coined by Spencer [2], as an informal definition of ‘natural selection’—the central concept of evolutionary theory—thereby elevating the term ‘fitness’ to one of the core concepts of his theory. Since then, the term ‘fitness’ has assumed tremendous importance in understanding biological phenomena. Nevertheless, the concept of ‘individual fitness’—the usual referent of such a term—has not yet been precisely defined. This unjustifiable gap has been masked by the existence of the definition of ‘genetic fitness’ proposed by Fisher [3] and Fisher [4], which deals with the relative fitness among different gene alleles. Indeed, when seeking the definition of ‘fitness,’ we frequently encounter this allele selection coefficient, as can be seen in [5-8], but we do not find a precise mathematical definition of the term applicable to individuals or lineages of individuals, even though both the origin and the relevance of the concept stem from this usage. The following text aims to fill this crucial gap in contemporary biology.

Introduction

The word “fitness” is commonly used in two distinct senses: potential fitness and actual (effective) fitness. I will clarify the differences while simultaneously proposing a definition for the effective fitness of an individual. A third use of the term applies to gene frequencies.

Potential fitness

It corresponds to our expectations about an individual’s life. If we encounter two individuals of the same species, one robust, the other small and frail, we are tempted to believe that the first will survive longer and have more descendants than the latter. However, such an expectation can be frustrated, for example, if the robust individual dies soon after due to any unforeseen event, so natural selection does not always occur as anticipated.

Not only chance but numerous other factors can frustrate our expectations regarding potential fitness. Let’s imagine a hypothetical scenario where two species of mammals coexist on the same island, and one exclusively feeds on the other. In such a case, we might assume that a mutant predator faster than other individuals of the species would be more fit and that this mutation would eventually prevail throughout the species. However, the increased speed of the predator caused by the mutation may disrupt the dynamic balance between populations, leading to the local extinction of the prey and consequently, of the predator. Thus, what seemed to favor the fitness of individuals ended up causing the entire population to go extinct on the island. A broad range of analogous idealizations illustrates the immense difficulty one would encounter when trying to rigorously define potential fitness.

Actual fitness

a) Asexually reproducing populations

In exclusively asexual populations, the actual, or effective, fitness of an individual can be described by the function φ(t), which corresponds to the number of its living adult descendants at a given moment. The individual should be included in the calculation if it is alive at the moment under consideration. Thus, in species exclusively reproducing asexually, the actual fitness of an individual is:

φ(t) = n + 1 Φ (1)

Where ‘n’ corresponds to the number of its living fertile descendants at the time ‘t’, plus 1, if the individual itself is alive; ‘Φ’ is the fitness unit and should be read as ‘fit’.

b) Sexually reproducing populations

The measurement of the actual fitness of sexually reproducing individuals is more intricate, thus, before introducing it, certain considerations are necessary.

In sexually reproducing populations, population stability is achieved if each individual produces two offspring. This is because, in sexually reproducing populations, each individual is, in a sense, only a “half-descendant” of each of its parents. For sexually reproducing populations to remain at equilibrium, each individual must, on average, produce two offspring before dying. In this case, each couple, on average, generates two descendants, ensuring that the number of pairs of individuals remains constant across generations. This suggests that the couple, and not the individual, should be considered the evolutionary unit.

The considerations above suggest the following measure for the actual fitness of sexually reproducing individuals: the fitness ‘φ’of individual ‘I₀’ during generation ‘g’ is the number of its living descendants ‘n’ divided by ‘2^g ’ (where ‘g’ is the number of generations separating the individual from its descendant).

$\phi \left[I_0\left(g\right)\right]=\frac{n}{2^g}\Phi \text{ (2)}$

This simplified calculation applies only to species subject to seasonal generations or other processes that result in the simultaneous death of all adults.

For usual populations, where different generations coexist, the fitness of an individual at time “t” should be expressed as:

$\phi \left[I\left(t\right)\right]={\displaystyle \sum _{d=1}^m\frac{1}{2^{g\left(d\right)}}}\Phi \text{ (3)}$

Where ‘d’ is the lineage connecting the individual to each of its living descendants, ‘m’ is the number of lineages, and ‘g(d)’ is the length of these lineages, i.e., the number of generations incorporated by the lineage.

This calculation resembles that of inclusive fitness [9]. The proposal will be clarified by the following example.

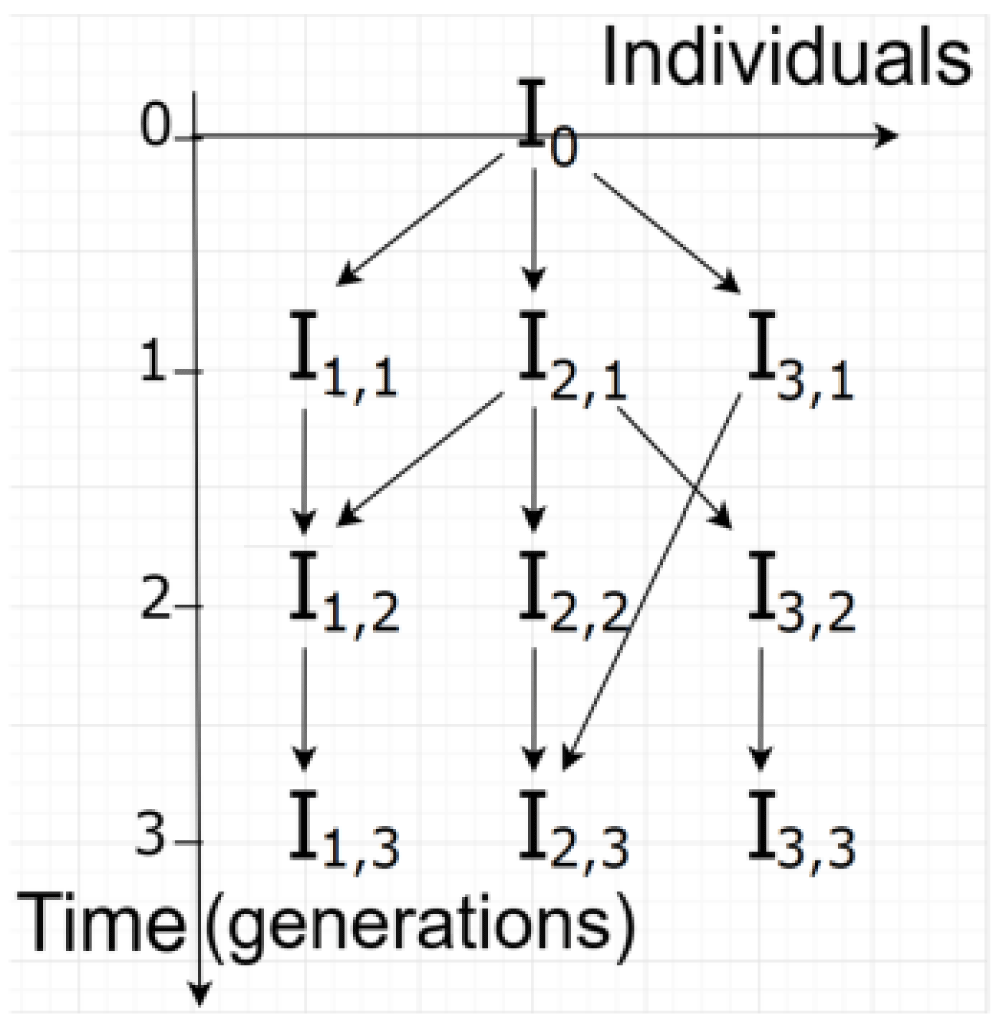
Figure 1 below depicts an individual and its descendants. Arrows indicate the lineages. All individuals are generated through sexual reproduction. Ancestors who are not descendants of the original individual have all been omitted, so when only one arrow points to an individual, its other parent has been omitted from Figure 1. Generations are not distinctly demarcated, as seen with individual ‘I_2,3’ which belongs simultaneously to generations 2 and 3. For simplicity, however, let’s consider that all individuals are born and die at the moment stipulated by the generation in which they occur, although individual ‘I_3,1’ from generation 1 has generated individual ‘I_2,3’ from generation 3.

The original individual, ‘I₀’, produced 3 individuals who lived during Generation 1. Each of these individuals descends directly from the original through a single lineage. Thus, if ‘I₀’ is deceased in generation 1, its fitness at that moment is:

Figure 1: The figure depicts an individual and its descendants.

$\phi \left[I_0\left(1\right)\right]=\frac{3\cdot 1}{2^1}\Phi =1.5\Phi \text{ (4)}$

This means that, in the first generation (t = 1), the individual ‘I₀’ has a fitness of 1.5 Φ. This value arises from the sum of the 3 descendant individuals of ‘I₀’in generation 1, each contributing 0.5 Φ. If the individual ‘I₀’ were alive at this moment, the value of 1, corresponding to its contribution, should be added to the total.

In the second generation, t=2, we can see that the individual ‘I_1,2’ is doubly descended from ‘I₀’ through ‘I_1,1’ and ‘I_2,1’. This individual, being doubly a grandchild of ‘I₀’ corresponds, for this reason, to two grandchildren, i.e., the son of ‘‘I1,1’and the son of ‘I_2,1’. Therefore, there are two lineages between ‘‘I₀’ and ‘I_1,2’ so the contribution of ‘I_1,2’ to the calculation of the fitness value of ‘I₀’ corresponds to twice the contribution of a common descendant from its generation, i.e.:

$\frac{2\cdot 1}{2^2}\Phi =\frac{1}{2}\Phi \text{ (5)}$

The contribution due to ‘I_2,2’is the same as that due to ‘I_3,2’and corresponds to half of the value of the contribution that would be given by its parent, ‘I_2,1’: ½² Φ = ¼ Φ. Thus, the fitness of ‘I₀(2)’ (actual fitness of ‘I₀’ in generation 2) corresponds to the sum:

$\phi \left[I_0\left(2\right)\right]=\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{2}\right)\Phi =1\Phi \text{ (6)}$

This calculation assumes the death of individuals from previous generations, so the contributions that would have been owed to them have not been computed.

In the third generation, we observe that the individual ‘I1,3’ descends from ‘I_1,2’ the double descendant of ‘I₀’ Its contribution to the actual fitness of ‘I₀’ is equivalent to half the contribution of its parent ‘I_1,2’ i.e., (¼) Φ.

The individual ‘I_2,3’ presents two peculiarities. It corresponds to two lineages of descent from ‘‘I₀’ and also belongs to two distinct generations. Its contribution to the fitness of ‘I₀’ must be calculated by summing the contribution from each lineage. These contributions, in turn, correspond to half the value of the contribution from each of its parents. Thus, the contribution of ‘I_2,3’ to the fitness of ‘I₀’ through ‘I_2,2’is 1/8 Φ, which is half the contribution of ‘I_2,2’ while the contribution through ‘I_3,1’ is ¼ Φ. The total contribution of ‘I_2,3’ then, adds up to 3/8 Φ to the fitness of ‘I₀’ at the time of the third generation. The contribution of ‘I_3,3’ to the fitness of ‘I₀’ is calculated simply as (½)₃ Φ = 1/8 Φ.

Therefore, the fitness of ‘‘I₀’ at the time of the third generation is determined by all its living descendants in the period and corresponds to:

$\phi \left[I_0\left(3\right)\right]=\left(\frac{1}{4}+\frac{3}{8}+\frac{1}{8}\right)\Phi =\frac{3}{4}\Phi \text{ (7)}$

Oscillation of an individual’s actual fitness value tends to occur for a short initial period, stabilizing after some time, if the population remains stable.

A special case: Haplodiploidy

For didactic reasons, certain previous considerations were imprecise. Strictly speaking, the proposed calculation does not arise from the mode of reproduction but from the portion of genetic material transmitted by the parent to each descendant. Half of the genetic material of each ancestor is typically passed on to descendants through sexual reproduction [10].

Hymenopterans, however, for example, reproduce unusually. Among them, females are diploid, while males are haploid. Unfertilized eggs develop into males, and fertilized eggs become females. In this mode, when a male reproduces, it occurs sexually. However, the calculation of their fitness must be conducted in the asexual mode, given that they pass on their entire genetic material to the offspring. Females, on the other hand, always pass on half of their genetic material to their offspring, whether through sexual or asexual reproduction. Thus, the calculation of their genetic contribution to each of their descendants must reflect this fact, and it should be divided by 2, regardless of whether it was generated sexually or asexually. The same should apply, then, to the fitness calculation, dividing the contribution of female descendants by 2 in each generation.

Relative fitness (of an individual about a group)

Populations are not always in equilibrium. While the proposed value above describes the absolute evolution of a lineage, it may be interesting, at times, to establish an individual’s fitness compared to others of the same species or group. This is especially desirable when analyzing species subject to cyclical population growth, and it can be done by introducing the following normalization factor:

${\phi }_{rel}\left(I,t\right)={\phi }_{abs}\left(I,t\right)\frac{P\left(t_0\right)}{P\left(t\right)}\text{ (8)}$

Where ‘φ_rel(I,t)’ is the relative fitness of individual ‘I’ at the time ‘t’, that is, the actual fitness of individual ‘I’ compared to others in the same group at the time ‘t’. ‘φ_abs(I,t)’ is the absolute fitness of ‘I’ at the time ‘t’. ‘P(t₀)’ is the initial population of the compared group measured at the time of the birth of ‘I’, and ‘P(t)’ is the population of the group at the time ‘t’.

For both modes of reproduction, a constant value of absolute fitness (φ_abs(I,t)) over time indicates that the total genetic contribution of individual ‘I’ remains constant throughout the period. The reduction in absolute fitness values implies a decrease in the genetic contribution of ‘I,’ while increasing values indicate its expansion over time. ‘φ_rel(I,t)’ —the relative contribution—shows the same pattern, although it analyzes the genetic contribution of the individual compared to others of the same species or group.

For purposes related to artificial life, primarily, we can define n-sexual reproduction, meaning n parents generating an individual.

In this context, ‘reproduction’ means the production of an individual similar to itself. ‘Sexual reproduction’ means the production of an individual inheriting characteristics from more than one parent, which differs from the traditional biological definition that involves meiosis.

For n-sexual reproduction, the contribution of each parent consists of the portion of characteristics inherited from them. The results of these contributions may differ from one individual to another, with some parents potentially contributing more than others to the inheritance of traits in the offspring.

Conclusion

Generalizing, we can define an individual’s fitness as the sum of each contribution owed to all its living descendants, which consists of the sum of the traits inherited by all living descendants at the considered moment. On the other hand, an individual’s participation in the reproduction of another, without its traits being reproduced, should be seen solely as a parasitic relationship. In this case, the individual contributing to the reproduction of another without reproducing any of its characteristics is a host, not a parent.

1. Darwin C. On the Origin of Species through Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. 5th ed. London: John Murray; 1869. p. 91–92. Retrieved February 22, 2009. “This preservation of favorable variations, and the destruction of injurious variations, I call Natural Selection, or the Survival of the Fittest.”
2. Spencer H. The Principles of Biology. 2 vols. New York: D. Appleton; 1864–1867. Reprinted by Williams and Norgate, Oxford University; 1914.
3. Fisher RA. On the dominance ratio. Proc R Soc Edinb. 1922;42:321–341.
4. Fisher RA. The Genetical Theory of Natural Selection. Oxford: Clarendon Press; 1930. Available from: http://dx.doi.org/10.5962/bhl.title.27468
5. Grafen A. Biological fitness and the fundamental theorem of natural selection. Am Nat. 2015;186:000-000. Available from: https://doi.org/10.1086/681585
6. Grafen A. Biological fitness and the Price equation in class-structured populations. J Theor Biol. 2015;373:62-72. Available from: https://doi.org/10.1016/j.jtbi.2015.02.014
7. Grafen A. The left-hand side of the fundamental theorem of natural selection. J Theor Biol. 2018;456:175–189. Available from: https://doi.org/10.1016/j.jtbi.2018.07.022
8. Hansen T. Fitness in Evolutionary Biology. 2018. Available from: https://www.preprints.org/manuscript/201804.0271/v1
9. Hamilton WD. The genetical evolution of social behavior. J Theor Biol. 1964;7(1):1-16. Available from: https://joelvelasco.net/teaching/167win10/hamilton64a-geneticalevolution1.pdf