Annals of Systems Biology
Application of (bio) chemical engineering concepts and tools to model genetic regulatory circuits, and some essential central carbon metabolism pathways in living cells. Part 4. Applications in the design of some Genetically Modified Micro-Organisms (GMOs)
Gheorghe Maria1,2*
2Romanian Academy, Chemical Sciences Section, Calea Victoriei 125, Bucharest 010071, Romania
Cite this as
Maria G (2024) Application of (bio) chemical engineering concepts and tools to model genetic regulatory circuits, and some essential central carbon metabolism pathways in living cells. Part 4. Applications in the design of some Genetically Modified Micro-Organisms (GMOs). Ann Syst Biol 7(1): 001-034. DOI: 10.17352/asb.000021Copyright License
© 2024 Maria G. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.In the first part of this work, the general Chemical and Biochemical Engineering (CBE) concepts and rules are briefly reviewed, together with the rules of the control theory of Nonlinear Systems (NSCT), all in the context of (i) deriving deterministic Modular Structured Kinetic Models (MSDKM) to describe the dynamics of metabolic processes in living cells, and (ii) of Hybrid Structured Modular Dynamic Models (HSMDM) (with continuous variables, linking the cell-nano-scale MSDKM state variables to the macro-scale state variables of the bioreactor dynamic model). Thus, in the HSMDM model, both prediction quality and its validity range are improved. By contrast, the current (classical/default) approach in bioengineering practice for solving design, optimization, and control problems based on the math models of industrial biological reactors is to use unstructured Monod (for cell culture reactor) or simple Michaelis-Menten (if only enzymatic reactions are retained) global kinetic models by ignoring detailed representations of metabolic cellular processes.
By contrast, as reviewed, and exemplified in the second part of this work, an accurate and realistic math modelling of the dynamic individual GERMs (gene expression regulatory module), or genetic regulatory circuits (GRC), and cell-scale CCM (central carbon metabolism) key-modules can be done by only using the novel holistic ’Whole-Cell Of Variable-Volume’ (WCVV) modelling framework, under isotonic/homeostatic conditions/constraints introduced and promoted by the author. An example was given in the same Part 2 for the case study of a dynamic model for the oscillating glycolysis coupled with the Tryptophan (TRP) oscillating synthesis in the E. coli cells.
As exemplified in the present paper, the use of an HSMDM (WCVV) model can successfully simulate the dynamic of cell individual GERMs, and of GRC-s (i.e. operon expression here), simultaneously with the dynamics of the bioreactor. Among multiple advantages - state-variables prediction, of a higher accuracy, and detailing degree, over a wider time-range for the bioreactor dynamic parameters (at both macro- and nano-scale level);
As exemplified here, the immediate applications of such an HSMDM model are related to solving difficult bioengineering problems, such as (i) in-silico off-line optimization of the operating policy of the bioreactor, and (ii) in-silico design/checking some GMOs of industrial use and able to improve the performances of the target bioprocess.
Note
Part 1: (General concepts) of this paper is in-press with Current Trends in Biomedical Eng & Biosci., (Juniper, Irvine CA, USA), 22(1), 556080-556104 (2023), DOI: 10.19080/CTBEB.2023.22.556080
Part 2: (Mathematical modelling framework) of this paper will soon appear in Annals of Reviews & Research, (Juniper publ, Irvine CA, USA)
Part 3: (Applications in the bioengineering area) of this paper will soon appear in Archives in Biomedical Engineering & Biotechnology, (Iris publ, San Francisco CA, USA), 2023, ISSN: 2687-8100.
If parts 2 and 3 are not available, the reader is asked to consult the references [1-4].
Abbreviations and notations
aG: G-L-specific interfacial area; aL: L-G -interfacial area (identical to aG); aS: L-S-specific interfacial area; Aj: Atomic (molecular) mass of species j; a,b: Rate constants in the Hill-type kinetic expression; Cj: Species j concentration; Dj: Diffusivity of species j in a certain phase; D: Cell content dilution rate (i.e. cell-volume logarithmic growing rate); db: Bubble average diameter; dp: Particle diameter; dr: Reactor diameter; F: Feed flow rate; FL: Liquid feed flow-rate; g: Gravitational acceleration; [ ]: Concentration of the mercury ions in the liquid (bulk) phase of the bioreactor; Km: Michaelis-Menten constants; KG: G-L mass transfer coefficient (on the gas side); KH: Henry constant; KL: L-G mass transfer coefficient (on the liquid side); KS: L-S mass transfer coefficient (on the liquid side); k: Rate constants; nH: Hill-coefficient; nPD,nPR: Partial orders of reaction; nj: number of moles of species j; ns: number of species in the cell; NA: Avogadro number; p: overall pressure; Pj: Partial pressure of species j; ---Reynolds number (liquid); Rg: universal gas constant; rj: species j reaction rate; : Schmidt number (liquid); : Sherwood number; T: Temperature; t: time; tc: cell-cycle time; uG: Gas superficial velocity; uL: Liquid superficial velocity; V: Volume; vm: Maximum reaction rate; X: Biomass in the bioreactor; Yj: Molar ratio of species j to the rest of the species in the mixture
Greeks
α,ω: Stoichiometric coefficients; β,: Constants used in the evaluation of particle effectiveness in Table 8; εG: Volume fraction of the gas in the bed; εL: Volume fraction of the liquid in the bed; εp: particle porosity; εs: volume fraction of particles in the bed; Φ: Optimisation objective function; φ: Thiele modulus; ϕC: Carman shape factor (Trambouze et al., 1988); ηj: effectiveness factor of reaction j; µL: Dynamic viscosity of the liquid; ρ: Density; π: osmotic pressure; σ: interfacial tension; ΣL: power dissipated per unit mass of liquid; τp: particle tortuosity
Superscript
*: Saturation
Index
App: Apparent; cell: Referring to the E. coli cell; cyt: cytoplasma; ef: effective; env: environment; G: referring to gas, or at the G-L interface; in: inlet; L: referring to liquid, or at the L-G interface; max: maximum; o: initial; p: particle; ref: reference value; s: referring to particle, or at liquid (L) – solid (S) interface, or referring to the steady-state; trans: referring to the transport.
Abbreviations
DAE: Differential-Algebraic Equations set; G-L: gas-liquid; G•: Gene; Gmer: mer plasmids generating mer operons in the cell; GmerX (or GX): mer genes (generic X, including 5 lumped genes denoted by G (lumped genome), GR, GT, GA, GD in (Figures 1-4); GRC: Genetic Regulatory Circuit; HSMDM: hybrid structured modular dynamic (kinetic) models; L-S: liquid-solid; MetG, MetP: Metabolites; M-M: Michaelis Menten; MM1, MM2, PHM: reduced (apparent) kinetic models given in Table 8; NADPH: nicotinamide adenine dinucleotide phosphate; NutG, NutP: Nutrients; nM: Nano-molar; ODE: Ordinary Differential Equations Set; P•: Protein; PmerX: mer proteins [generic P, including 5 lumped proteins denoted by P (lumped proteome), PR, PT, PA, PD in (Figures 1-4)]; QSS: Quasi-Steady-State; RSH: Compounds including thiol redox groups; S: Substrate; SCR: Semi-Continuous Reactor; TF: Transcription Factor; TPFB: Three-Phase Fluidized Bioreactor; WCVV: Variable Volume Whole-Cell; X: Biomass; [.]: Concentration”
1. Introduction
In the last decades, there has been a tendency to replace the complex processes of fine chemical synthesis, highly energy-consuming and generating large amounts of toxic waste, with biosynthesis processes (using isolated and purified enzymes, or cell cultures as bio-catalysts). The motivation is given by the multiple advantages offered by enzymatic processes [3]: i) very high selectivity; ii) very high conversion; iii) does not generate toxic by-products; iv) very mild reaction conditions, easy to achieve without high costs (low temperatures of 20-60°C, normal pressure, pH within controllable limits). Thus, in recent years, a significant number of enzymatic or biological industrial processes have been reported [5-8] to obtain chemical products/derivatives in the fine organic synthesis industry, the pharmaceutical industry, the food industry, or the detergent industry, by using various bioreactors with cell or enzyme cultures [5,8]. Among these new processes is the production of derivatives of monosaccharides, organic acids, alcohols, amino acids, etc., using mono- or multi-enzymatic reactors, or bioreactors with cell cultures used in the production of yeast, food additives, recombinant proteins (enzymes, vaccines), biopolymers [5,6,9]. The development of a sustainable biological process must consider several aspects related to the characteristics of the biocatalyst, the integration of the process and the minimization of costs, satisfying economic, environmental / safety, and social objectives [10-12].
When scale-up a new biological process (of known kinetics) several biochemical engineering problems must be solved, consisting of:
- Choosing the type of biological reactor most suitable for the studied bioprocess [6,13,14];
- Choosing the optimal mode of operation of the selected bioreactor (discontinuous BR; semi-continuous (fed-batch) FBR with a variable feeding; discontinuous with intermittent addition of biomass/substrate BRP; or continuous stirred tank reactor CSTR, with continuous feeding and evacuation of the liquid-phase (chemostat), etc. [6]);
- Choosing how to use the biocatalyst (biomass in a free state or immobilized on a suitable solid/gel support to increase its stability [13,14,16]). As discussed in the literature, the biocatalyst contributes the most to the production cost [3,16].
The importance of optimal operation of biological reactors
In the case of biological reactors (with free, or immobilized biomass), the trend in the biosynthesis industry is to use complex systems, with more efficient genetically modified micro-organisms (GMO), and employ sophisticated but efficient immobilization systems, which prevent premature inactivation of the biomass due to mechanical and chemical stress from the bioreactor environment. Thus, modern biological processes, together with the multi-enzymatic ones, prove to be very effective in the biosynthesis of numerous chemical compounds, thus competing in terms of efficiency with organic chemical synthesis, proceeding with high selectivity and specificity, by reducing consumption of energy and generating less environmental pollution [3]. This characteristic of industrial biosynthesis is exploited for various economic purposes (industry, medicine, environment, agriculture, fuel production) [17,18]. In this context, the in-silico derivation of an optimal operating policy of the industrial bioreactors becomes a challenging engineering problem.
As reviewed in the literature [1-4,19-22], and shortly in the Part-1 of this work, the in-silico (math/kinetic model-based) numerical analysis of biochemical or biological processes, by using the CBE concepts / numerical rules is proved to be not only an essential but also an extremely beneficial tool for engineering evaluations aiming to determine the optimal operating policies of complex multi-enzymatic reactors [9,23-26], or bioreactors [3,4,6,19,27,28].
Among these numerical tools, is the deterministic modular structured cell kinetic models (MSDKM - with continuous variables, based on cellular metabolic reaction mechanisms). and the hybrid structured modular dynamic models (HSMDM) (with continuous variables, linking the cell-nano-scale MSDKM state variables to the macro-scale state variables of the bioreactor dynamic model) are the essential ones., proved by the exponential-like increase in the reported applications in the last decades.
In Part-2 of this work, special attention is paid to the authors’ contributions related to the dynamics simulation of the Gene Expression Regulatory Modules (GERM) and of Genetic Regulation Circuits/Networks (GRC/GRN) in living cells, by introducing and promoting the concepts of a novel dynamic modelling framework of the cell processes, that is the so-called “WHOLE-CELL VARIABLE CELL VOLUME” (WCVV) for isotonic/homeostatic cell systems. The advantages of using the more realistic WCVV math modelling approach to simulate the cell metabolic processes have been proved and shortly reviewed when building-up dynamic modular models of CCM-based syntheses, and GRC-s inside living cells.
The MSDKM models can also be used to evaluate the cell metabolic fluxes, thus assisting the in-silico design of GMOs. This area belongs to the border field of Synthetic Biology defined as “putting engineering into biology” [29]. By inserting new genes (plasmids) or knock-out some of them, modified CCM / GRC-s can be obtained inside a target micro-organism, thus creating a large variety of mini-functions / tasks (desired ‘motifs’) to the mutant (GMO) cells in response to external stimuli [3,4,30-50].
Translation of the CBE and NSCT concepts/rules (see Part 1-2 of this work) in Systems Biology, Computational biology, and Bioinformatics is leading to obtaining extended structured cellular kinetic models MSDKM including nano-scale state variables adequately representing the dynamics of the cell key-reaction-modules. If the MSDKM model is further linked to those of the bioreactor macro-scale dynamic model, the result is the HSMDM dynamic model that can satisfactorily simulate, for instance, the self-regulation of the cell metabolism and its adaptation to the changing bioreactor environment, utilizing complex GRC-s, which include chains of individual GERMs. The HSMDM kinetic models are related to solving various difficult bioengineering problems, such as (i) in-silico off-line optimization of the operating policy of various types of bioreactors, and (ii) in-silico design/checking some GMOs of industrial use, able to improve the performances of several bioprocess/bioreactors.
Besides, the use of extended HSMDM models presents multiple advantages, such as (i) a higher degree of accuracy and the prediction detailing for the bioreactor dynamic parameters (at a macro- and nano-scale level); (ii) the prediction of the biomass metabolism adaptation over tens cell cycles to the changing conditions from the bioreactor; (iii) prediction of the CCM key-species dynamics, by also including the metabolites of interest for the industrial biosynthesis (Part 2, [4,5]); (iv) prediction of the CCM stationary reaction rates (i.e. metabolic fluxes) allow to in-silico design GMO of desired characteristics.
As proved by Maria [1-4,51], and Yang, et al. [52], the modular structured kinetic models can reproduce the dynamics of complex metabolic syntheses inside living cells. This is why, the metabolic pathway representation of GRC and CCM in dynamic models, with continuous and/or stochastic variables seems to be the most comprehensive mean for a rational design of the regulatory GRC with desired behaviour [53]. The same MSDKM can satisfactorily simulate, on a deterministic basis, the self-regulation of cell metabolism for its rapid adaptation to the changing bioreactor reaction environment, using complex GRC-s, which include chains of individual GERMs.
As exemplified in Parts 3 and 4 of this work, the MSDKM and HSMDM models (developed under the novel WCVV math modelling framework) can simulate the dynamics of the bioreactor simultaneously with those of the cellular metabolic processes occurring in the bioreactor biomass.
This work is aiming at proving, by using a relevant case study, the feasibility, and advantage of using the relatively novel HSMDM concept by coupling the GRC-based cell structured deterministic nano-scale models with the macro-scale state-variables of the analyzed bioreactor. The resulted hybrid dynamic model was successfully used for engineering evaluations and to design a GMO E. coli.
For more case studies on using MSDKM and HSMDM models, under the WCVV modelling framework, the reader is asked to consult the following works [3,4,55-58]:
- In-silico design of a genetic switch in E. coli with the role of a biosensor [3,4,54-58];
- An HSMDM math model able to simulate the dynamics of the mercury-operon expression in E. coli cells, and its self-regulation over dozens of cell cycles, simultaneously with the dynamics of the macro-level state variables of a semi-continuous reactor (SCR) of a Three-Phase Fluidized Bioreactor Type (TPFB). The same extended model was used for the in-silico designing of cloned E. coli cells (with variable mer-plasmid concentrations) aiming at maximizing the biomass capacity of mercury uptake from wastewaters [59-62]. This case study is also approached here.
- An HSMDM math model able to simulate the dynamics of key-species of the CCM of E. coli cell coupled with the simulation of the macro-scale state variables of a Batch Reactor (BR). The HSMDM model was used for the in-silico design of a GMO E. coli with a maximized capacity of both biomass and succinate (SUCC) production. The used numerical techniques were those of the gene knock-out, and of the Pareto-front for multi-objective problems [30].
- The use of an HSMDM math model for the in-silico design of a GMO E. coli with a modified glycolytic oscillator [31-37,63-73]. The HSMDM model can be further extended, becoming the core of a modular dynamic model used to simulate the CCM and regulation of various metabolite syntheses, with application to in silico reprogramming of the cell metabolism to design GMO of various applications [3,4,32,74]. One example is the in-silico off-line optimization of the operating conditions of a fed-batch bioreactor (FBR) with GMO E. coli to maximize the production of tryptophan (TRP). Thus, compared to a simple batch bioreactor (BR) using a wild E. coli cell culture, the TRP production was increased by 73% (50% due to the in-silico design of a novel GMO E. coli strain, and 23% due to the model-based off-line optimization of the variable feeding of the FBR). [3,4,27,31,34,71,75]. Complex MSDKM structured models including CCM and GRC modules are able to predict conditions for oscillations occurrence for various cell processes [1-4,31-34,37,51, 52,63,64,]. As studied by Yang et al. [52], “all biochemical reactions in organisms can not occur simultaneously due to constraints of thermodynamic feasibility and resource availability, just as all trains in a country cannot run simultaneously. Therefore, oscillations provide overall planning and coordination for the inner workings of the cellular system. This seems to be contrary to the theoretical basis of genome-scale metabolic models (GEMs), which are based on the steady-state hypothesis and flux balance analysis [76], but just as computers will not operate in the same way as the human brain, this difference can be understood and accepted, so that non-equilibrium theory and the steady-state hypothesis have been and will continue to coexist and guide our reasoning.”[52] (see also Part 3 of this work).
- The use of an extended HSMDM math model to simulate the dynamics of the nano-scale CCM key-species, and of the Tryptophan (TRP)-operon expression, and its self-regulation, together with the dynamics of the macro-scale state-variables of a FBR including genetically modified E. coli cultures. Eventually, this dynamic model was used to design/check a GMO E. coli and to determine the multi-control optimal operating policy of a bioreactor (FBR) to maximize the Tryptophan (TRP) production [3,4,27,33-36,74,75,77-86]. (See also Part 3 of this work).
- An MSDKM math model able to simulate the dynamics of key-species of the CCM of E. coli cells involved in the synthesis of Phenyl-alanine (PHA). The HSMDM model was used to in-silico re-configure the metabolic pathway for Phenyl-alanine synthesis in E. coli [54] to maximize its production. That implies modifying the structure and activity of the involved enzymes, and modification of the existing regulatory loops. Searching variables of the formulated mixed-integer nonlinear programming (MINLP) multi-objective optimization problem are the followings: the regulatory loops (that is integer variables, taking a “0” value when the loop has to be deleted, or the value “1” when it has to be retained); the enzyme expression levels (that is continuous variables), and all these in the presence of the stoichiometric and thermodynamic constraints. To solve this complex optimization problem, two contrary objectives are formulated: maximization of the PHA selectivity, with minimization of cell metabolites’ concentration deviations from their homeostatic levels (to avoid an unbalanced cell growth). The elegant solution to the problem is the so-called Pareto-optimal front, which is the locus of the best trade-off between the two adverse objectives. Choosing two problem-solution alternatives from this Pareto-curve [3,54] is to observe the large differences between the two pathways into the cell, fully achievable by using genetic engineering techniques to produce desirable GMOs.
- A HSMDM model to simulate the dynamics of the key species and the FBR state variables used for monoclonal antibodies (mAbs) production. This extended dynamic model was used for the in-silico off-line derivation of the multi-objective optimal control policies to maximize the mAbs production in an industrial FBR [6].
2. The use of a hybrid WCVV-GRC structured kinetic model to optimize a SCR-TPFB bioreactor used for mercury uptake from wastewaters by immobilized E. coli cells cloned with mer-plasmids
The case study purpose – an overview
This section 2 exemplifies the use of a complex HSMDM to solve an engineering problem at an industrial pilot scale, that is the use of a complex cell WCVV structured kinetic model of the mer-operon GRC expression (Figure 1) in an HSMDM model to optimize a pilot-scale semi-continuous (SCR) TPFB bioreactor (Figure 2) used for mercury uptake from wastewaters by immobilized E. coli cells cloned with mer-plasmids. The developed HSMDM dynamic model links the cell-scale model part (including the dynamics of the nano-scale key-state variables/species) to the biological reactor macro-scale key-state variables for improving the both model prediction quality and its validity range. Eventually, the HSMDM model was used to in-silico design a GMO (i.e. an E. coli cloned with mer-plasmids in a degree to be determined) for improving its capacity for mercury uptake from wastewaters (Figure 3).
The {cell + TPFB} HSMDM dynamic model of the E. coli cloned bacterium can simulate the self-control of the GRC responsible for the mer-operon expression, and predict
- The influence of the TPFB bioreactor control variables [such as the feed flow-rate (FL), the mercury ions concentration [ ]in in the feeding liquid], and the biomass concentration in the bioreactor [X];
- The influence of various bioreactor running parameters [such as the size of the solid porous particles (dp) of pumice on which the biomass was immobilized; the concentration [Gmer] of the mer-plasmids used in the cloned E. coli cells) on the bioreactor’s performance to uptake the mercury ions from wastewaters and in eliminating these ions as mercury vapours entrained by the continuously sparged air into the bioreactor [3,4,7,59-62,87].
This HSMDM dynamic model is a worthy example of applying WCVV models, and the GERMs properties (P.I.-s) described in Part 2 of this work, to adequately represent a complex modular GRC-s for the mer-operon expression in E. coli cells. The structured GRC-WCVV model was proposed by Maria [59-61] to reproduce the dynamics of the mer-operon expression in Gram-negative bacteria, such as E. coli, and Pseudomonas sp., for the uptake of mercury ions from wastewaters under various environmental conditions. The complex structured dynamic modular model was constructed and validated by using the Philippidis et al. [88-90] experimental data, and the Barkay et al. [91] information on the mer-operon expression characteristics.
Finally, this structured cellular GRC model was included in an HSMDM dynamic model of the SCR-TPFB bioreactor by Maria et al. [59-62] to simulate its dynamics over a wide range of operating conditions, that is FL = [0.01-0.04] L/min.; [ ]in = [10-40] mg/L; [X] =[250-1000] mg/L; dp = [1-4] mm; [Gmer] = [3-140] nM.
As evidenced by this application, the current trend in bioengineering is to use multi-layer (hybrid) HSMDM models [3,4,92] to extend the detailing degree of the developed bioreactor dynamic models, by also including the dynamics of the concerned cell key-species metabolism. Exemplification is made in this section by coupling an unstructured dynamic model of a TPFB, used for mercury uptake from wastewaters by immobilized E. coli cells, with a cell simulator of the GRC controlling the mercuric ion reduction in the bacteria cytosol. The obtained results reported:
- A significant improvement in the model prediction quality (ca. 3%-12% in state variables, and up to 40% in reduction rate vs. experimental information);
- A significant improvement in the detailing degree [i.e. simulation of 26+3 (cell + bulk) state-variable dynamics (nano- and macro-levels) by the HSMDM model vs.- only 3 (bulk, macro-level) state-variable dynamics by the overall unstructured Monod / Michaelis-Menten kinetic model]. The major advantages of the hybrid HSMDM model come from the possibility of predicting the bacteria metabolism adaptation to environmental changes over a large number of cell generations (cell cycles), and also the effect of cloning cells with certain plasmids to modify its behaviour under stationary or perturbed conditions.
This section exemplifies the possibility of coupling an unstructured TPFB dynamic model including macro-scale state variables [93] used to simulate the dynamics of the mercury uptake by immobilized E. coli cells on pumice milli-meter size support, with a structured E. coli cell model of Maria [59-62]. The advantage of using such a hybrid (bi-level) modelling approach is related to the improvement of the prediction accuracy of the reactor performance/state variable dynamics, and of the prediction of the bacteria metabolism adaptation to environmental ‘step’-like changes in the environmental mercury content [ ]env through the modelled cell GRC related to the mer-operon expression, and by mimicking the whole-cell growth under balanced conditions.
If successful, such an approach can support the idea of
- Improving the bioreactor performances, by employing an off-line in-silico (model-based) multi-objective optimization procedure to determine the optimal operating policy of the bioreactor [59-62];
- Improving the quality of process monitoring (control), by using an optimal operating policy determined with a reduced unstructured dynamic model obtained by lumping the extended HSMDM model [9,59,87];
- In-silico design cloned E. coli with an increased content of mer-plasmids. Such a facility is offered only by the complex HSMDM dynamic model of increased predictive power. In general, such in-silico investigations to design GMOs are supported by the tremendous improvement in the computing power over the last decades, and by the continuous expansion of the available information from cellular bio-omics databanks (see Parts 1-2 of this work), despite steady efforts necessary to elaborate such detailed HSMDM cellular numerical simulators.
Exemplifications of such modular GRC models used for the in-silico design of GMOs–s of industrial use include several case studies discussed by Maria [1-4,92] (Figure 5), and in Part 3 of this work. Due to the cell metabolism complexity, and the existence of control parameters at the cell-level (related to the strain phenotype), but also at the bioreactor macro-level (control state-variables), in-silico optimization of an industrial bioprocess by using GMOs often translated in a multi-objective optimization problem [27,30,34,35,55,59-62,74]. Such an optimization problem is difficult to solve by using common numerical algorithms. A couple of case studies exemplify their own positive experience with using HSMDM including cell structured models of CCM, and of various GRC-s for optimizing industrial bioreactors, or for the design of some GMO–s for improving certain bioprocesses of practical interest are presented in Parts 3 and 4 of this work, and by Maria [1,2,3,4,27,30,33,36,59-61,74,92].
Mercury ion reduction in bacteria cells – the apparent kinetics
”Bacteria resistance to mercury is one of the most studied metallic-ion uptake and release processes (see the review of Barkay et al. [91]) due to its immediate large-scale application for mercury removal from industrial wastewaters [93-94]. The bacteria response to the presence of toxic mercuric ions in the environment is surprising. Instead of building carbon- and energy-intensive disposal ’devices’ into the cell (like chelate-compounds) to ’neutralize’ the cytosolic mercury and thus maintain a tolerable level, a simpler and more efficient defending system is used. The metallic ions are catalytically reduced to the volatile metal , less toxic, and easily removable outside the cell (as in the liquid environment of the TPFB) by simple cell membranar diffusion. Such a process involves fewer cell resources and is favoured by the large content (milli-molar concentrations) of low molecular-mass thiol redox buffers (RSH) able to bond and transport in the cytosol as Hg(SR)2 and of NAD(P)H reductants able to convert it into neutral metal . (see the overall reactions in Table 1). A genetic regulatory circuit (GRC) responsible for the involved mer-operon expression controls the whole process, by including seven genes of individual expression levels of 7 encoded proteins, of which expression is induced and adjusted according to the level of mercury Hg (SR)2 and other metabolites into the cytosol (Figure 1). The whole process is tightly cross- and self-regulated to hinder the import of too large amounts of mercury into the cell, which eventually might lead to the blockage of cell resources (RSH, NADPH, key-metabolites, and key- proteins), thus compromising the whole cell metabolism.
While the role of each mer-gene and mer-protein in the mercury ion reduction process is generally known, not all the regulatory loops of the mer-operon expression are perfectly understood, and the way by which the cell adapts itself to variations of mercuric ion concentrations in the environment. Philippidis et al. [88-90] proposed a reduced apparent (unstructured, global) kinetic model, of the Michaelis-Menten (M-M) type, to quickly simulate the main steps of mercury uptake by E. coli, that is the membranar transport of environmental into the cell (of rt rate) and its reduction (rP rate, see Table 1). To highlight the slowest process step, separate experiments have been conducted with cultures of intact cells or ’permeabilized’ cells (with a more permeable cell membrane to metallic ionic species). The results clearly showed that membranar permeation is the rate-controlling step, being one order of magnitude slower than the cytosolic mercuric ion reduction. Identification of rate constants of the two main reactions for cloned E. coli cells with an increasing copy number of mer-plasmids, in the range of [Gmer] = 3-140 nM, compared to those identified for [Gmer] = 1-2 nM (for wild-types of E. coli) reveals the following aspects (Table 1):
- The rate constants are strongly dependent on the mer-plasmid (genes) level in the cloned cells of E. coli, the real reaction mechanism inside the cell being more complex than those suggested by the two apparent reaction rates (rt and rP) of Philippidis et al. [88-90];
- Such reduced/global kinetic models can approximately represent the overall mercury uptake by the cells, and the steady-state process efficiency, being useful for the bioprocess scale-up engineering quick but rough calculations [93];
- The unstructured models can not represent the mer-GRC response to various inducers, the cell response to stationary or dynamic perturbations in the mercury level ( = ) in the bioreactor liquid-phase, and in its quasi-constant feeding. Also, the apparent M-M kinetic model can not explain and simulate/predict the self-regulation of the whole transport-reduction process, how the mer-gene expression is connected to the cell volume (biomass) growth, and the cell content dynamics and replication;
- When an immobilized biomass alternative is used, several global Michaelis-Menten simplified kinetic models (denoted by MM1, MM2, PHM) were proposed by Deckwer et al. [93] (Table 8). By including these reduced global models in the TPFB bioreactor model (Table 7), the rapp mercury reduction apparent reaction rate results.
The TPFB bioreactor reduced model (with global kinetics) and its nominal operating conditions
To exemplify the construction of an un-structured dynamic model for the approached mercury removal process, the TPFB bioreactor of Deckwer et al. [93] was approached. The main characteristics and the nominal operating conditions of this TPFB bioreactor under a semi-continuous (SCR) operation are presented in Table 2 (with biomass immobilized on pumice), and Table 6 (with biomass immobilized on pumice). As a first step in the engineering analysis of this TPFB bioreactor, it is important to emphasize, the requirement that the elaborated math model should be able to simulate the mercury removal under a wide range of operating conditions (especially those related to the mercury inlet concentration [ ] in ). Besides, the dynamic model must include the ranked influential factors on the mercury uptake efficiency in the approached TPFB bioreactor for further operating decisions.
The used lab-scale TPFB bioreactor (Figure 2, and Figure 3, up-right) includes a resistant E. coli cell culture. The bioreactor is completely automated being able to maintain its control parameters of [Table 2 (pumice), and Table 6 (alginate)] at their optimal set-point, by ensuring a constant pH, temperature, a constant inlet feed flow-rate, and inlet mercury concentration [ ] in, a constant sparkling air inlet feed flow-rate, and a constant concentration of nutrients used as C/N/P source for the biomass optimal growth.
Initially, to study this bioprocess, Deckwer et al. [93] used E. coli bacteria immobilized on alginate beads (Table 6 (alginate)), but further tests have been extended by using immobilized biomass on porous pumice granules of 0.9 mm to 4 mm diameter (Table 2 (pumice)). The pumice carrier checked in the present paper is particularly attractive, the carrier exhibiting a high BET area and porosity, and a large pore size (even higher than 10 µm), thus allowing a good diffusion of the substrate (mercuric ions) to the cells from inside the support. The operating conditions are tightly controlled, that is the liquid flow rate, the aeration rate (pO2), pH, and the temperature required by an equilibrated bacteria growth [Table 2(pumice), and Table 6 (alginate)]. The sufficient supplied oxygen guarantees a good cell metabolism and a high content of cytosolic NADPH necessary for mercury reduction. Besides, the continuously bubbling air plays also the role of volatile metallic mercury carrier, by removing it from the liquid system. Eventually, the mercury vapours from the air leaving the system are condensed and recovered [93]. A background pollution of ca. 100 nM is considered in the input water (that is ca. 0.02 mg/L, which is smaller than the metabolic regulation threshold of 0.05 mg/L), thus maintaining active the mer-operon into the E. coli cell. The biomass content of the support is variable (ca. 0.6-3 gX/L, according to [93,96], but a quasi-constant level of ca. 1 gX/L can be maintained by employing a purge/renewal system for the solid particles. At an industrial scale, when treating polluted waters, the outlet gas (air) from the bioreactor, containing the volatile metallic mercury, is passed through an adsorption device, or a de-sublimation system allowing the recovery of metallic mercury [97].
To simulate the (semi-)continuous TPFB bioreactor performance, a simple unstructured dynamic ideal model was considered (Table 7), as a first approach [98,99], by assuming homogeneous (perfectly mixed) liquid and gas phases, and a uniform distribution of the solid particles (of uniform characteristics) in the G-S-L fluidized bed. This reduced TPFB bioreactor dynamic model accounts for only the apparent (Michaelis-Menten) mercury uptake kinetics (denoted by MM1, MM2, PHM) of Deckwer et al. [93] (Table 8). For such global kinetics, the apparent mercury reduction rate (rapp) necessary in the bioreactor model (Table 7) is evaluated following the (Table 8) rule. The apparent rate was evaluated by solving on every integration time-increment the quasi-steady-state equality of mass fluxes at the solid-liquid (S-L) external interface (on the liquid side), by also including the external diffusion coefficient KSaS [100]. This rule also includes the diffusional resistance of the substrate (mercury ions) / product (dissolved metallic mercury) transport through the support pores.
If the apparent (Michaelis-Menten) mercury uptake kinetics of Philippidis et al. [88-90] (Table 1) are introduced in the TPFB bioreactor model, then a better unstructured global model is obtained (Table 3). By also including the [Gmer]-dependent rate constants, it results in the apparent mercury reduction rate (rapp) by the immobilized bacteria of concentration cX in (Table 1) in the spherical solid carrier [of fraction εs in Table 2 (pumice)] for different levels of [Gmer] plasmids. The mercury mass balance in the liquid and gas phases is presented in (Table 7). This reduced (unstructured) TPFB reactor dynamic model (Table 7, and Table 8) includes terms referring to the mass balance in the bulk (liquid, L) phase, the gas phase (G), the interphase L-G transport (rtrans) of the volatile mercury, and the overall/apparent bioprocess of mercury reduction inside the solid particles (rapp). In such a way, the apparent mercury reduction rate also includes the diffusional resistance of the substrate (mercury ions) / product (dissolved metallic mercury) transport through the pumice support pores.
A hybrid reduced/unstructured dynamic model of the TPFB can by constructed by linking the macro0scale state-variables of the TPFB (Table 7), with the Michaelis-Menten kinetics of Philippidis et al. [88-90] (Table 1). This apparent model (Figure 6) can only give a rough idea of the bioreactor dynamics, but it is unable to describe the biomass adaptation to environmental changes, that is variations in both inlet feed flow-rate and inlet mercury load in the influent. To offer a prediction to such engineering requirements, a structured kinetic model of the mercury uptake in the E. coli bacteria at a cellular level is necessary. The next chapter describes the complex HSMDM structured model proposed by Maria [59-61], by considering the macro-level TPFB model linked to the cell biological process included by using the WCVV modelling approach (Part 2 of this work) to simulate the dynamics of the cell mer-operon expression self-regulation in the wild, or modified E. coli under various environmental (bioreactor operating) conditions.
The resulting unstructured TPFB global dynamic model of (Table 7), while keeping the apparent M-M kinetics of (Table 8) only for the mercury cytosolic reduction step, allows a rough simulation of the transient operating conditions of the TPFB bioreactor. This apparent model of (Figure 6, plus Table 8), even if suitable for quick/rough engineering evaluations, is unable to describe the biomass adaptation to environmental changes, that is variations in the both inlet feed flow rate and inlet mercury load in the influent, or the effect of cloning E. coli cells on the bioreactor efficiency.
Extended HSMDM model of the TPFB bioreactor
To avoid the above-mentioned limitations of the unstructured / reduced dynamic model of the TPFB bioreactor, an extended and complex HSMDM structured model was elaborated by also including the effect of cloning E. coli with various concentrations of mer-plasmids [Gmer], by also including the Michaelis-Menten [Gmer]-dependent kinetics of Philippidis et al. [88-90] in the cytosolic mercury reduction step (Table 4).
To offer a prediction to such engineering requirements, an extended HSMDM structured kinetic model of the mercury uptake in the E. coli bacteria at a cellular level is necessary (of WCVV type, see Part-2 of this work). And, of course, this cell-state-variables (nano-scale) part of the HSMDM should be linked to the TPFB bioreactor state-variables (macro-scale), because they are interrelated.
This section describes the WCVV-type structured cell model proposed by Maria [59-61] to simulate the dynamics of the mer-operon expression induction by the presence of environmental mercury, and the expression self-regulation in the “wild”, or in-silico design GMO E. coli under various environmental (bioreactor operating) conditions.
This HSMDM structured and modular cell kinetic model has been developed by Maria [59-61]. Roughly, the part of the extended HSMDM structured model referring to the mer-operon expression WCVV model includes a GRC of 7 GERMs (Figure 1) linked by following the rules described in this section, and by accounting for the few experimental information of Philippidis et al. [88-90], and of Barkay et al. [91]. The derived GRC model can simulate the dynamics of the mer-operon expression, and the process self-control at a molecular level under isothermal and isotonic conditions.
The extended HSMDM structured bioreactor bi-level model includes two inter-connected parts: (a) The macro-level state-variables of the TPFB bioreactor (Table 3), that is the mass balance of , in the liquid-phase, and of in the gas-phase; (b) The cell nano-level state-variables, that is the mass balance of the cell key-species included in the WCVV-GRC model of (Table 4), completed with the [Gmer]-dependent apparent Michaelis-Menten kinetics of (Table 1) for the mercury reduction reaction in the cell cytosol. All the cell parameters included in the HSMDM model correspond to the E. coli characteristics (Table 5), and (Figure 12).
The macro-scale state variables
More specifically, the mercury differential mass balance, in the TPFB model of (Table 3) includes the following terms:
- The apparent mercury reduction rate, evaluated at the solid interface;
- The substrate (that is S = = ) diffusional transport in the particle, expressed by the effectiveness factor (h) evaluated using the Thiele modulus for a Michaelis-Menten type reaction [101], the effective diffusivity (DS,ef) accounting for the molecular diffusion (DS,L), the particle porosity (ep) and the tortuosity (t) (other resistances being neglected [102]);
- The apparent rate rj, app was evaluated by solving on every integration time-increment the quasi-steady-state equality of mass fluxes at the solid-liquid (S-L) external interface (on the liquid side), by also including the external diffusion coefficient kSaS [100]. This rule also includes the diffusional resistance of the substrate (mercury ions) / product (dissolved metallic mercury) transport through the support pores.
- The liquid-to-gas transport rate rtrans of the metallic mercury ( ), evaluated from the quasi-steady-state equality of mass fluxes at bubbles G-L interface, by accounting for the mass transfer coefficients kLaL (on the liquid film side; experimental value adopted), and kGaG (on the gas film side; evaluated from the Sharma’s relationship given by Trambouze et al. [99] ).
The cell-scale state variables
This paragraph describes the WCVV structured cell model proposed by Maria [59-61] to simulate the dynamics of the mer-operon-induced expression, and its self-regulation under various environmental conditions. This model was constructed and validated by using the experimental data of Philippidis et al. [88-90], and the experimental information of Barkay et al. [90] on the mer-operon characteristics. The WCVV cell model was built up by accounting for the GERMs library, their P.I.-s, and the linking rules presented in Part 2 of this work.
The proposed E. coli cell model by Maria [59-61] includes the GRC responsible for the control of the mer-operon expression and the whole process of mercury ions removal. The proposed GRC includes 4 lumped genes (denoted by GR, GT, GA, GD in (Figure 1, Figure 2, Figure 3, and Figure 4) of individual expression levels induced and adjusted according to the level of mercury and other metabolites into the cytosol. As it follows from these figures, the mer-operon expression process is induced by the presence of a small concentration of mercury ions in the environment, leading to the appearance in the cytosol as Hg(SR)2 compounds. The whole process is tightly cross- and self-regulated to hinder the import of large amounts of mercury into the cell, which eventually might lead to the blockage of cell resources (RSH, NADPH, other metabolites, and proteins), thus compromising the whole cell metabolism. The GRC model includes four GERMs of simple but effective [G(PP)1] type (see the discussion of Part-2 of this work) as follows (see Figure 11, and Table 4):
- A GERM to regulate the Hg2+ transport across the cellular membrane, mediated by three proteins (PmerP, PmerT, and PmerC) from the periplasmatic space, considered as a lumped permease PT in the model. Phillippidis et al. [88-90] found this transport step to be energy-dependent and the rate-determining step for the whole mercury uptake process. Once the mercuric ion complex arrives in the cytosol, thiol redox buffers (such as glutathione of millimolar concentrations) form a dithiol derivative Hg(SR)2. Instantly, the GT lumped gene expression is induced by the regulatory protein PR, and easily ‘smoothed’ by the large ‘ballast’ effect of the proteome lump P. (see rule 6 of chapter. 2.3.6 of Part-2 of this work).
- A GERM to control the expression of the PR protein that induces and controls the whole mer-operon expression in the presence of cytosolic (even if they are present in traces, that is low nM concentrations, (Table 5) and Figure 12). This GERM acts as an amplifier of the mer-expression leading to a quick (over ca. 30 s) cell response by starting the mer-enzymes production. First, the expression of the GR gene leads to obtaining the encoded PR protein. The process magnitude is also controlled by the protein PD, present in small amounts in the cell.
- A GERM to control the expression of PA enzyme responsible for the Hg(SR)2 (that is ) reduction to metallic mercury ( ) into the cytosol. The metallic mercury is relatively non-toxic for the cell, being easily removable through membranar diffusion into the bioreactor bulk liquid phase ( ). From here, metallic mercury ( ) passes into the gas phase (air bubbles) , being entrained and continuously removed by the sparged air as mercury vapours ( ), to be later recovered. The GA gene expression is induced and controlled by the PT protein, whose expression is controlled by the PR level, which in turn is controlled by the cytosolic mercury and PD levels.
- A GERM controlling the protein PD synthesis. This protein has a complex role, by maintaining a certain level of GR expression even when the mercury is absent in the cytosol [91]. It also hinders the over-expression of GR and GT when too large concentrations of mercury are present in the environment.
- A GERM controlling the replication of the lumped cell proteome (P) and genome (G) (of concentrations 107 nM, and 4500 nM, respectively, to mimic the effect of “cell ballast”, see Part-2 of this work) in the immobilized E. coli cells. These data are based on the Ecocyc [103] databank (Table 5, and (Figure 12), thus mimicking the cell ’ballast’ effect on the cell genes expression, and on all considered reactions. The need to include the cell content lump (the so-called ’cell ballast’) in the WCVV model is legitimate by the possibility offered by such a structured cell model to reproduce the smoothing effect of perturbations leading to more realistic transient times (compared to a cell with a ‘sparing’ content), the synchronized response to certain inducers, and the ‘secondary perturbation’ effect transmitted via the cell volume to which all cell components contribute (see the discussion in the Part-2 of this work).
- Thus, the whole mer-operon expression consists of a controlled expression in cascade (Figure 11) of all 4 mer-genes {GR, GT, GA, GD in (Figure 1, Figure 2)}.
In total, the cell GRC dynamic model describing the mer-operon expression includes only 26 individual or lumped cellular species involved in 33 reactions (Figure 1, Figure 11, and Table 4). The structured cell WCVV model is presented in the (Table 4). The cell model is coupled with the SCR –TPFB dynamic model (Table 3) through the rj,app link to the individual reactions occurring inside the cell. The WCVV cell model includes not only the reactions and the dynamics of the mer-GRC, but also the enzymatic reactions directly responsible for the environmental mercury (also denoted by ) import into the cell as , and for its reduction to cytosolic metallic mercury in the E. coli cells cloned with a defined [Gmer] concentration of mer-plasmids.
All reactions in the cell model of (Table 4) are considered elementary, except some of them for which extended experimental information exists, that is [59-61]:
- A Michaelis-Menten rate expression for the mercuric ion permeation through the membrane into the cell;
- A Michaelis-Menten rate expression for the mercuric ion reduction in the cytosol;
- A Hill-type quick induction of the GR expression that can rapidly initiate the production of permease PT (through the control protein PR) when mercuric ions are present in large amounts.
- Dimmerization reactions of TF-s are considered to be much more rapid than the enzyme synthesis, while equal concentrations of active gene (G) and inactive (GPP) forms of the generic gene G are considered at homeostasis to maximize the GERM efficiency (see Part-2 of this work) (Figure 1, and Figure 11).
- The lumped proteome P, present in a large amount, is included in all gene expression rates, thus leading to a more realistic evaluation of the GERM regulatory efficiency indices P.I.-s (see Part-2 of this work) [1,2,3,4,57,58].
- The WCVV model equations for the mercury uptake in E. coli, together with the general hypotheses of the WCVV model are presented in (Table 4). The cell is considered an open system, of uniform content and negligible inner gradients. To not increase the number of parameters, the structured model includes GERM of the simplest form [G(PP)1] (see Part-2 of this work) for all mer-genes, by using dimeric TF-s (of Protein: Protein type) to increase the GERM regulatory efficiency, as experimentally proved by [1,2,3,38,55,58]. The resulting HSMDM model includes 26 individual or lumped cellular species and 33 reactions. All reactions are considered elementary, except some of them for which extended experimental information exists, that is the Michaelis-Menten rate expression for mercury permeation into the cell, and its reduction in cytosol. A Hill-type induction of the GR expression is adopted to rapidly amplify the mer-operon expression when mercuric ions are present in significant amounts inside the cell. Dimerization reactions of TF-s are considered to be much more rapid than the enzyme synthesis, while equal concentrations of active (G(i)) and inactive (G(i): TFTF) forms of the generic gene G(i) are considered at homeostasis to maximize the GERM efficiency [1,2,3,4,55]. The homeostatic characteristics of E. coli cells (belonging to a uniform culture) from the reactor, and the adopted species concentrations are presented in (Table 5).
- The model rate constants are estimated from solving the cell stationary mass balances for nominal concentrations of observable species (see Part-2 of this work), but also from optimizing the GERM regulatory indices (see Part-2 of this work), for instance: (1) by adjusting the optimum TF level of gene expression to obtain the minimum recovering times after a 10% dynamic perturbation in one of the key species, and (2) realize the smallest sensitivities of the homeostatic species concentrations vs. external perturbations (see Part-2 of this work for an extended discussion). The E. coli cell characteristics and the considered cell key-species homeostatic concentrations used in the rate constants estimation are given in (Table 5). Exceptions are the Michaelis-Menten (M-M) rate constants for the mercury transport and its reduction in cytosol adopted from the Phillipidis et al. [88-90] kinetic data. By adopting this M-M reduced model, the rate constants of these two metabolic steps depend on the amount of [Gmer] plasmids in the cloned E. coli cells (Figure 11, and Figure 6). Simple correlations are used to include this essential aspect in the model.
HSMDM structured model advantages
As extensively discussed in Part 2 of this work, and proved in this section, such a cell WCVV structured model presents a large number of advantages, being able to:
- Simulate the cell metabolism adaptation when the environmental mercury level changes. Such a reconfiguration of the levels of mer-genes and mer-proteins is presented in (Figure 13) as a step response after a ‚step’-like perturbation in the mercury level from []s = 0.1 µM to 10 µM (ca. 2 mg/L), in a cloned E. coli cell with mer-plasmids of [Gmer]= 140nM, compared to a cell cloned with only [Gmer]= 3 nM. The transient state toward the cell’s new homeostasis of the “adapted” mer-gene/protein levels stretches over 15-20 cell cycles (of ca. 0.5 h each) as long as the environment stationary step perturbation is maintained. An E. coli cell with a higher content of mer-plasmids reacts much strongly to the environmental perturbations, by quickly starting to produce the enzymes responsible for the mercury removal.
- Because the Hg2+ reduction rate constants are dependent on the mer-plasmid level in the cell, the WCVV GRC model can predict the maximum level of mer-plasmids that can be added to the cell genome for improving its mercury uptaking capacity without exhausting the internal cell resources, thus putting in danger the cell survival. Consequently, it follows that this cell MSDKM model allows the in-silico design of modified E. coli cloned with a suitable amount of mer-plasmids to improve its efficiency in cleaning wastewater by improving the mercury uptaking capacity. As an example, (Figure 14 presented the cell key-species stationary levels, and the mercury concentration in the TPFB bioreactor bulk-phase for two GMOs: An E. coli cloned with [Gmer] = 67 nM, and another culture of E. coli cells cloned with [Gmer] = 140 nM. Simulations of Maria [59-62] revealed that as the mer-plasmids level increases, the mercury uptake capacity also increases. However, an upper limit exists (around 140 nM) over which the cell resources will be exhausted, putting its metabolism in danger.
- The simulated state-variables plotted in (Figure 14), for using the unstructured global model (Table 7 and Table 8) comparatively with using the structured extended HSMDM model, reveal a higher quality (vs.- experimental data), and more detailed/refined predictions for a larger number of state-variables.
- By coupling the structured MSDKM cell model of (Table 4) with the three-phase (TPFB) continuous bioreactor model of Table 3 (with immobilized E. coli cells on pumice beads; see also the bioreactor model in Figure 6), Maria et al. [59-62] have been able to determine the optimal operating policies of the bioreactor in relationship to the culture of cloned E. coli cells. Similar studies are reported by [7,59-62,88].
Quick comparison between the structured HSMDM and the unstructured/global dynamic model of the TPFB reactor:
The superiority of the structured extended HSMDM model (Table 3 and Table 4) against the unstructured reduced model (Table 7 and Table 8) was used to simulate the TPFB dynamics over a wide range of time.
Thus, when simulating the TPFB reactor performance (of nominal conditions given in Table 2, for the biomass immobilized on pumice support) by employing a classical unstructured reactor model, the biomass adaptation to variable input loads is not accounted for, that is the maximum rates vm,t, vm,P, and the Michaelis inhibition constants Kmt, KmP and KiP of (Table 1) are kept constant (eventually depending only on the Gmer plasmid level). In fact, vm,t and vm,P rate constants depend on the cell enzyme levels of PA (reductase) and PT (permease) (Figure 1), which vary during the bacteria adaptation in the bioreactor under stationary or transient conditions.
To solve this problem by also offering a more detailed and robust prediction on the system dynamics/cell metabolism evolution, more detailed (structured) dynamic models are necessary for the TPFB bioreactor, linked to the structured kinetic model of mer-GRC in E. coli cell. Thus, it results in the here-described hybrid structured HSMDM model. The two linked differential models are solved together simultaneously, by applying a mutual exchange of input/output parameters {[ )], [ ], PT, PA} on every small time increment throughout the solution (integration) of the HSMDM model, as graphically represented in (Figure 1).
As described in the below paragraph dedicated to solving the HSMDM model of (Table 3 and Table 4)., due to its structure, only the HSMDM model can simulate the E. coli cell response to dynamic or stationary perturbations from the environment (i.e. the TPFB bulk-phase). And also the influence of [Gmer] plasmids on the bioreactor performances. For instance, (Figure 13) displays the E. coli cell adaptation after a ‘step’-like perturbation in the environmental [ ]s (that is in the bioreactor bulk-phase) from the background level of 0.1 µM to 10 µM (ca. 2 mg/L), for the case of cell cloned with [Gmer]= 3 nM (full line), or with [Gmer]= 140 nM (dash line) mer-plasmids. The transient state toward the cell’s new homeostasis usually lies over 15-20 cell cycles as long as the environmental stationary perturbation is maintained. The simulated species dynamic trajectories plotted in (Figure 13) reveal a vigorous response of the cell mer-species (especially of PT, and PA) to the perturbation in the environmental [ ]s (i.e. liquid bulk-phase). Such cell responses to environmental perturbations are impossible to reproduce by the simple unstructured reduced model (Table 7 and Table 8). A more detailed comparison between the structured HSMDM model, and the unstructured/global one, for this case study is made by Maria [3,4].
The link between the macro-, and cell-scale state variables when solving the HSMDM model
The link between the two parts of the macro-sate-variables and the cell-state-variables of the HSMDM is made by the [ ] controlling the [ ], which, in turn, will control the whole mer-operon dynamics and the mercury reduction process through the cascade expression of the key-proteins {PR, PT, PA, PD} (see Table 4). In turn, the cell bioprocess induced and intensified by the [ ] level, controls the TPFB bioreactor output [ ] through [ ], via [ ].
The link between the bioreactor macro-state variables and the cell nano-scale-state variables can be better pointed out when describing the HSMDM DAE model solution, that is its integration over a large time domain.
Due to its high complexity, the solving rule of the HSMDM model involves successive integration steps with an adopted time-interval equal to the cell cycle (ca. 30 min), enough to obtain the steady-state of the TPFB reactor on every time-interval, as follows: (i) The rule starts with solving the extended hybrid HSMDM E. coli cell model by using the known initial condition (the cell variables’ initial state, or those from the end of the previous integration cycle), and by considering the current concentration of [ ] in the bioreactor liquid phase (the nutrients are considered in excess and of constant levels). Thus, the cell species dynamics over one cell cycle are obtained from solving the WCVV cellular model. (ii) Then, the TPFB reactor model is solved over the current time-interval by using the known initial conditions (i.e. the reactor state variables from the end of the previous time-interval), and by considering the enzymes PT and PA concentrations resulting from the E. coli model solution. The [PT] and [PA] are necessary for setting the maximum reaction rates in the reactor model. The biomass level on the support is taken constant in the simulated case study, but an additional mass balance can be easily added to the reactor model if a kinetic model about biomass (X) growth is available.
The procedure is repeated a large number of times, over hundreds of cell cycles. For instance, (Figure 13) displays the E. coli cell adaptation after a ‘step’-like perturbation in the environmental [ ]s (that is in the bioreactor bulk-phase) from the background level of 0.1 µM to 10 µM (ca. 2 mg/L), for the case of cell cloned with [Gmer]= 3 nM (full line), or with [Gmer]= 140 nM (dash line) mer-plasmids. The transient state toward the cell’s new homeostasis usually lies over 15-20 cell cycles as long as the environmental stationary perturbation is maintained. The simulated species dynamic trajectories plotted in (Figure 13) reveal a vigorous response of the cell mer-species (especially of PT, and PA) to the perturbation in the environmental [ ]s (i.e. liquid bulk-phase). Such cell responses to the environmental (dynamic or stationary) perturbations are impossible to reproduce by the simple unstructured reduced model (Table 7 and Table 8).
Some simulations with the HSMDM extended dynamic model
The resulting hybrid dynamic HSMDM model of (Table 3), including the WCVV kinetic model of the GRC responsible for the mer-operon expression of (Table 4) allows simulating with more accuracy the dynamics of the TPFB bioreactor at both macro- and (call) nano-scale level. By also including in (Table 4) the Michaelis-Menten kinetics of Philippidis et al. [88-90], the above-described extended HSMDM model can also be used to study the parametric sensitivity of the studied TPFB. Thus, the dynamics of the TPFB (with the characteristics of (Table 2(pumice)) have been simulated under the nominal operating conditions of Table 2, but every time-varying one operating parameter, that is:
- The inlet [ ]in concentration from the background pollution level (0.02 mg L-1) to successively 1, 5, or 10 mg L-1 levels (Figure 7);
- The inlet liquid flow rate FL of 0.01, 0.02, and 0.04 L/min (Figure 8);
- The biomass load cX on the solid support taken as 0.1, 0.25, 1.0 gX/L (referred to as the liquid volume) for a constant fraction of the solid in the reactor (Figure 9);
- The use of particle average diameter dp of 1 mm, or 4 mm respectively (Figure 10).
Simulations of the TPFB with this extended HSMDM model over ca. 50 min running time reveal that the liquid residence time in the reactor (related to the inlet liquid flow rate, FL) and the biomass content (cX) are the most influential operating parameters, being directly responsible for the realised mercury uptake conversion. For instance, by doubling the feed flow rate (from 0.02 to 0.04 L min-1), the uptake conversion can be reduced by ca. 5%. The particle size is also important, with an increase in the average dp leading to a higher resistance to the diffusional transport in pores and to a particle effectiveness diminishment (from 0.51 for dp = 1 mm to 0.15 for dp = 4 mm under nominal conditions). On the other hand, the biomass average load in the reactor can be adjusted by employing a continuous purge-renewal system of the solid particles. The mercury content in the input flow, [ ]in in the range of 1-40 mg/L, has a significant influence on the mercury content of the output gas (Figure 7). As further proved, this last parameter is also of tremendous importance for adaptation of bacteria metabolism when using “wild” E. coli cells, or those cloned with an increased copy-numbers of mer-plasmids (denoted by [Gmer]).”
In-silico design of a cloned (GMO) E.coli.
Simulations with the extended HSMDM model of the TPFB dynamics using several E.coli cultures, that is E.coli cells cloned with various levels of mercury-plasmids, reveal interesting conclusions. As plotted in Figure 15, the cellular uptake process (i.e. the stationary reduction rate, rHg ) may be improved by increasing the mer-permease (PT) content into the cell (GT/PT dynamics in Figure 14-right), up to a limit of ca. [Gmer] = 80-140 nM mer-plasmids, higher than the permeation rate remains unchanged, thus preventing exhaustion of the cell metabolic resources. Such a conclusion was experimentally confirmed by Philippidis et al. [88-90]. As revealed by the present simulations, for the same reason, the cell regulatory system maintains an upper limit for the membranar transport rate (rt) of environmental into the cell, irrespectively to the concentration in the environment, the cytosolic concentration never exceeding a 3500-5000 nM level (Figure 13).
Fitting the HSMDM model parameters from experimental data
To overcome the high computational effort necessary to fit the large number of rate constants of this extended HSMDM model, and to increase their confidence and physical meaning, a three-step procedure was employed based on the available experimental data and additional information from literature, as followings.
- Mass transport parameters of the TPFB reactor, that is interfacial partial transfer coefficients (kSaS, kLaL, kGpG), effective diffusivity (Def) and particle effectiveness factor (h) have been estimated by using the experimental data of Deckwer et al. [93], and based on common correlations from the chemical engineering literature (Table 3) evaluated for the specified reactor operating conditions of (Table 2- pumice support).
- Cell model parameters are estimated by using the Philippidis et al. [88-90] kinetic data obtained from separate batch experiments with “wild” (not-cloned) E. coli cells. By using the defined cell nominal characteristics of (Table 5) (some key notations are: tC = cell cycle time; Vcyt,O = born cell volume; CX = biomass concentration in the bioreactor; P = cell lumped proteome; G = cell lumped genome; NutG, NutP = lumped nutrients for G and P synthesis, respectively; [Gmer] = mer-plasmid levels into the cloned cell. The stationary levels of the essential cell mer-proteins (PA, PR, PD) are taken from the literature data. The involved TFs (PRPR, PTPT, PAPA, PDPD) intermediate concentrations resulted by maximizing the GERMs regulatory efficiency P.I.-s (see Part-2 of this work) [1,2,3,4,21,22]. The resulting rate constants of (Table 4) have been estimated for the most severe experimental conditions of [ ]s = 120 µM, and [Gmer] = 140 nM. The used first guess of Hill-induction rate constants (nPD = 1, nPR = -0.5, nH = 2, a = 3) have been adopted at values recommended in the literature, by similarity with the Hill-induction of gene expression in genetic switches (see the remarks included in Table 4), while the Michaelis-Menten rate constants of mercury membranar transport (rmax,t,Kmt) and its reduction rates’ constants (rmax,P, KmP, KiP) have been kept at the fitted values of Philippidis et al. [88-90] (Table 1). The reference concentration CHg2cy,ref was adopted at the average cytosolic level of mercuric ions detected by Philippidis et al. [88-90]. When applying the model estimation rule, the GERM regulatory indices have been kept at their optimized levels, which corresponds to: (i) Equal concentrations of catalytically active/inactive forms [G(j)]s = [G(j)TFn]s adopted at steady-state to ensure GERM maximum regulatory efficiency vs. perturbations (i.e. smallest sensitivities of the homeostatic levels vs. external perturbations [1-4], and (Part-2 of this work); (ii) adjustable optimum [TF]s level (ca. 4 nM here; Table 5) involved in the gene expressions to get the minimum recovering times after a dynamic perturbation in the key species [1,2,21,22,51,58], (see Part-2 of this work). Other adjustable parameters, such as the cell concentration in biomass (Ccell), are tuned to fit the experimental cellular mercury reduction rate of Philippidis et al. [88-90].
- The model validity is extended over a wider experimental range, by covering the input [ ] = 0-100 mg/L, and plasmid levels of [Gmer] = 3-140 nM. All these have been realised by adjusting some key parameters of the extended HSMDM model, and by applying two concomitant fitting criteria, that is: (1) the cytosolic mercury reduction rate should fit the experimental values of Philippidis et al. [88-90], obtained for ‚permeabilized’ cells (i.e. Min , see the r8 expression of Table 4); (2) the TPFB reactor predicted output CHg,Out by the unstructured model (Table 1, Table 7, and Table 8) with using the Philippidis et al. [88-90] Michaelis-Menten parameters and the mass transfer terms, to fit with those of the structured (cell + reactor) extended HSMDM model of (Table 3, and Table 4). The Hill parameter b=2a4 was adjusted by using the following approximate linear dependence on the inlet mercury load:
(see the fitted values amin and amax in Table 4 – footnote d). The above-simplified correlation tries to account for the influence of the environmental mercury on the induction characteristics of the mer-operon expression, that is a slow induction in the presence of low levels of Hg2+ inducer and a sharp (sigmoidal) mer-operon expression response to high levels of [ ] inducer. When a certain saturation level is reached, the limited cell resources will impose ’flattening’ the metabolic mer-rates and the mer-protein levels, irrespectively to the increased amount of mercury in the environment [88-90].
The extended HSMDM model predictions are in satisfactory agreement with the experimental data. Thus, the model predictions for rHg in (Figure 15, A-C) (curves ’2’) roughly fall within the confidence band [‚Eup’, ‚Elow’] of the experimental curves (‚E’) of Philippidis et al. [88-90] for three different cloned cell cases (confidence curves being plotted by taking constant the reported maximum relative error of ca. 19%). The unstructured model (chap.2.3, Table 1, Table 7), and Table 8) predictions (that is curves ’1’) reported apparent rHg of low adequacy, that is too low values. Such a result for the unstructured reduced model of the TPFB bioreactor is due to the rough bioprocess representation by the M-M model, and due to the inclusion of the mass transport resistance between the three phases in contact. The extended HSMDM model adequacy in terms of standard error ’Std’ / average observed value ’Obs’ ratio is evaluated for every cloned cell culture, leading to Std/Obs of 22.3%, 16.7%, 20.4%, 19.9%, 18.8% for [Gmer] levels of 3, 67, 78, 124, and 140 nM respectively, that is acceptable values when compared to the maximum experimental error (ca. 25-33% in Figure 15). The predicted structured vs. unstructured model outputs, in terms of outlet concentration of mercury ( ) are also in fair agreement (curves not displayed here), that is Std/Obs values of 3.0%, 4.7%, 3.7%, and 12% for [Gmer] levels of 67, 78, 124, and 140 nM respectively. The model’s poor adequacy for the [Gmer] = 3 nM data set and low [ ] in the environment (input) might be explained by the use of a less adapted E. coli cell than probably those studied by Phillipidis et al. [88-90], reflected by a smaller [PA] initial level of 600 nM (see the PA-curve in Figure 15-D). Once a higher level of Gmer-plasmids is introduced into the cell, then, when higher stimulus levels are present in the environment, the cytosolic PA level is tripling.
The extended HSMDM structured model cellular rate constants (see the above point (b), and Table 4) are in good agreement with the reported data from the literature, as remarked in the same (Table 4). The fitted rate constants multiplied by the reactant lead to reaction rates of the same order of magnitude as those reported in the literature for similar genetic processes, such as the TF (repressor monomer) dimerization, the TF binding to gene operator, or the mRNA (genes) synthesis reactions (Table 4) [59-61]. This observation sustains the physical meaning of model parameters, thus increasing the HSMDM model robustness.
As a final observation, by extending the detailing degree of the bioreactor dynamic model at a cellular level, the resulting structured HSMDM model not only preserves but also extends the adequacy of the unstructured model, adding the possibility to predict the cell species/fluxes dynamics over dozens of cell cycles. By offering details on the cell metabolism adaptation, the ’intrinsic’ reduction rate, and the possibility to in-silico predict the modified (cloned) cell response to various stimuli, such an HSMDM model presented in this paper is superior compared to the unstructured (apparent) bioreactor dynamic models. Eventually, the extended HSMDM models are worth the supplementary experimental and computational effort to derive/identify them.
Conclusions
Meritorious structured deterministic CCM kinetic models have been reviewed by Maria [2]. Deterministic kinetic models using continuous variables have been developed by Maria [3] for the glycolysis, and by [77,104-107] for the CCM in bacteria of industrial interest. Such models can adequately reproduce the cell response to continuous perturbations, the cell model structure and size being adapted based on the available –omics information. Even if such extended structured models are currently used only for research purposes, being difficult to identify, it is a question of time until they will be adapted for industrial / engineering purposes in the form of reduced HSMDM models.
In other words, this work presents a holistic “closed loop” approach that facilitates the control of the in vitro through the in silico development of dynamic models for living cell (biological) systems [108], by deriving deterministic modular, structured cell kinetic models (MSDKM), with continuous variables, and based on cellular metabolic reaction mechanisms.
The ever-increasing availability of experimental (qualitative and quantitative) information, at the cell metabolism level, but also about the bioreactors’ operation necessitates the advancement of a systematic methodology to organize and utilize these data. The resulting HSMDM was proved to successfully solve difficult bioengineering problems. In such HSMDM models, the cell-scale model part (including nano-level state variables) is linked to the biological reactor macro-scale state variables for improving the both model prediction quality and its validity range. The case study presented and discussed here proves this engineering aspect. An alternative compromise is to use hybrid models that combine unstructured with structured process characteristics to generate more precise predictions (see the review of Maria [74]). Hybrid models use a two-level hierarchy: the bioreactor macroscopic state variables linked with the nano-scale variables describing the cell key metabolic processes, and those of practical interest.
As proved by the case study presented in this paper, and by some additional ones mentioned in the Introduction section of this work, the use of MSDKM and HSMDM models (developed under the novel WCVV modelling framework) to simulate the dynamics of the bioreactor and, implicitly, the dynamics of the key cellular metabolic processes (CCM-based, related GRC-s, and target metabolites syntheses) occurring in the bioreactor biomass, presents multiple advantages, such as: (i) a higher degree of accuracy and the prediction detailing for the bioreactor dynamic parameters (at both macro- and nano-scale level); (ii) the prediction of the biomass metabolism adaptation over tens of cell cycles to the variation of the operating conditions in the bioreactor; (iii) prediction of the CCM key-species dynamics, by also including the metabolites of interest for the industrial biosynthesis; (iv) prediction of the CCM stationary reaction rates (i.e. metabolic fluxes) allow to in-silico design GMO of desired characteristics.
The superiority of structured HSMDM models is proved by several case studies approached by the author and briefly mentioned in the Introduction section of this paper. For details, the reader is asked to consult the above-indicated references.
However, to avoid the intensive experimental and computational efforts necessary to develop an extended structured HSMDM model, unstructured dynamic models of bioprocesses continue to be used for various engineering purposes. Even if of low precision, the unstructured/global models for the bioreactors and the conducted bioprocesses continue to be largely used in the engineering practice, for a quick design, optimization, or control of the industrial bioprocesses. For instance, for the case study mentioned in this paper, a method was presented to optimize the operating policy of a SCR bioreactor by using the reduced unstructured hybrid model. Maria [4,62,92].
This work was supported in part by U.S. Public Health Service grant AI-21862 and a grant from the MacArthur Foundation.
- Maria G. A review of some novel concepts applied to modular modelling of genetic regulatory circuits, Juniper publ., Irvine, CA, USA. 2017. https://juniperpublishers.com/ebook-info.php
- Maria G. Deterministic modelling approach of metabolic processes in living cells - a still powerful tool for representing the metabolic process dynamics, Juniper. publ., Irvine, CA, USA. 2017. https://juniperpublishers.com/ebook-info.php
- Maria G. In-silico design of Genetic Modified Micro-organisms (GMO) of industrial use, by using Systems Biology and (Bio)Chemical Engineering tools, Juniper publ., Irvine, CA, USA. 2018. https://juniperpublishers.com/ebook-info.php
- Maria G. Hybrid modular kinetic models linking cell-scale structured CCM reaction pathways to bioreactor macro-scale state variables. Applications for solving bioengineering problems, Juniper publ. Irvine, CA, USA, 2023. (open-access), in-press (galley-proofs).
- Liese A, Seelbach K, Wandrey C. Industrial biotransformations, Wiley-VCH, Weinheim. 2006.
- Maria G. Model-Based Optimization of a Fed-Batch Bioreactor for mAb Production Using a Hybridoma Cell Culture. Molecules. 2020 Nov 30;25(23):5648. doi: 10.3390/molecules25235648. PMID: 33266156; PMCID: PMC7729860.
- Scoban AG, Maria G. Model-based optimization of the feeding policy of a fluidized bed bioreactor for mercury uptake by immobilized P. putida cells. Asia-Pacific Journal of Chemical Engineering. 2016; 11(5): 721-734. DOI: 10.1002/apj.2003.
- Ghose TK, Fiechter A, Blakebrough N. Advances in Biochemical Engineering. Springer Verlag, Berlin. 1977-1978; 7-10.
- Straathof AJJ, Adlercreutz P. Applied biocatalysis. Harwood Academic Publ., Amsterdam. 2005.
- Jiménez-González C, Woodley JM. Bioprocesses: modeling needs for process evaluation and sustainability assessment. Comput. Chem. Eng. 2010; 34: 1009-1017.
- Khamseh AAG, Miccio M. Comparison of batch: fed-batch and continuouswell-mixed reactors for enzymatic hydrolysis of orange peel wastes. Process. Biochem. 2012; 47: 1588-1594.
- Tsangaris DM, Baltzis BC. Evaluation of batch and semi-batch reactor operation for enzymatic reactions with inhibitory kinetics. Chemical Engineering Science. 1996; 51: 2757-2762.
- Basso A, Serban S. Overview of Immobilized Enzymes' Applications in Pharmaceutical, Chemical, and Food Industry. In: Guisan, J., Bolivar, J., López-Gallego, F., Rocha-Martín, J. (eds), Immobilization of Enzymes and Cells. Methods in Molecular Biology Humana. New York. 2020; 2100. https://doi.org/10.1007/978-1-0716-0215-7_2
- Górecka E, Jastrz?bska M. Immobilization techniques and biopolymer carriers, Biotechnol. Food Sci. 2011; 75 (1): 65-86. http://www.bfs.p.lodz.pl
- Mara C. Studies on industrial reactor optimization involving complex multi-enzymatic systems, PhD thesis, Univ. Politehnica of Bucharest. 2019. (in Romanian).
- Nedovic V, Willaert R. Applications of cell immobilisation technology. Springer verlag, Amsterdam. 2005.
- Buchholz K, Hempel DC. From gene to product (Editorial), Eng. Life Sci. 2006; 6: 437-437. https://doi.org/10.1002/elsc.200690012
- Hempel DC. Development of biotechnological processes by integrating genetic and engineering methods. Eng. Life Sci. 2006; 6:443-447. doi: 10.1002/elsc.200620149
- Maria G, Gijiu CL, Cri?an M, Maria C, Tociu C. Model-based re-design of some genetic regulatory circuits to get Genetic Modified Micro-organisms (GMO) by using engineering computational tools (a mini-review), Current Trends in Biomedical Engineering & Biosciences. 2019; 18(3): 555988. DOI: 10.19080/CTBEB.2019.18.555988.
- Maria G, Maria C, Tociu C. A comparison between two approaches used for deterministic modelling of metabolic processes and of genetic regulatory circuits in living cells, U.P.B. Sci. Bull., Series B - Chemie. 2018; 80(1): 127-144. http://www.scientificbulletin.upb.ro/, WOS:000428112600010
- Maria G, Scoban AG. Setting some milestones when modelling gene expression regulatory circuits under variable-volume whole-cell modelling framework. 1. Generalities, Revista de Chimie (Bucharest). 2017; 68(12): 3027-3037. WOS:000423261900064
- Maria G, Scoban AG. Setting some milestones when modelling gene expression regulatory circuits under variable-volume whole-cell modelling framework. 2. Case studies, Revista de Chimie(Bucharest). 2018; 69(1): 259-266. WOS:000425369600053
- Maria G. Enzymatic reactor selection and derivation of the optimal operation policy, by using a model-based modular simulation platform. Comput. Chem. Eng. 2012; 36: 325-341. DOI: 10.1016/j.compchemeng.2011.06.006
- Maria G, Crisan M. Operation of a mechanically agitated semi-continuous multi-enzymatic reactor by using the Pareto-optimal multiple front method. J. Process Control. 2017; 53: 95-105. DOI: 10.1016/j.jprocont.2017.02.004
- Maria G, Pept?naru IM. Model-based optimization of mannitol production by using a sequence of batch reactors for a coupled bi-enzymatic process - A dynamic approach. Dynamics-Basel-MDPI. 2021; 1:134-154. https://doi.org/10.3390/dynamics1010008
- Maria G, Renea L, Maria C. Multi-objective optimization of the fed-batch bi-enzymatic reactor for mannitol production. Dynamics-Basel-MDPI. 2022; 2: 270-294. DOI: 10.3390/dynamics2030014
- Maria G, Renea L. Tryptophan Production Maximization in a Fed-Batch Bioreactor with Modified E. coli Cells, by Optimizing Its Operating Policy Based on an Extended Structured Cell Kinetic Model. Bioengineering (Basel). 2021 Dec 10;8(12):210. doi: 10.3390/bioengineering8120210. PMID: 34940363; PMCID: PMC8698263.
- DiBiasio D. Introduction to the control of biological reactors. In: Shuler, M.L. (ed.), Chemical engineering problems in biotechnology. American Institute of Chemical Engineers. New York. 1989; 351-391.
- Heinemann M, Panke S. Synthetic biology--putting engineering into biology. Bioinformatics. 2006 Nov 15;22(22):2790-9. doi: 10.1093/bioinformatics/btl469. Epub 2006 Sep 5. PMID: 16954140.
- Maria G, Xu Z, Sun J. Multi-objective MINLP optimization used to identify theoretical gene knockout strategies for E. coli cell. Chemical & Biochemical Engineering Quarterly. 2011; 25(4): 403-424.
- Maria G. Insilico derivation of a reduced kinetic model for stationary or oscillating glycolysis in Escherichia coli bacterium. Chemical & Biochemical Engineering Quarterly. 2014; 28(4): 509-529. doi: 10.15255/CABEQ.2014.2002
- Maria G. In silico Determination of Some Conditions Leading to Glycolytic Oscillations and Their Interference With Some Other Processes in E. coli Cells. Front Chem. 2020 Oct 28;8:526679. doi: 10.3389/fchem.2020.526679. PMID: 33195042; PMCID: PMC7655968.
- Maria G, Gijiu CL, Maria C, Tociu C. Interference of the oscillating glycolysis with the oscillating tryptophan synthesis in the E. coli cells. Computers & Chemical Engineering.2018; 108:395-407. https://doi.org/10.1016/j.compchemeng.2017.10.003.
- Maria G, Mihalachi M, Gijiu CL. Model-based identification of some conditions leading to glycolytic oscillations in E. coli cells. Chemical and Biochemical Engineering Quarterly. 2018; 32(4): 523-533. doi: 10.15255/CABEQ.2018.1300.
- Maria G, Mihalachi M, Gijiu CL. Chemical engineering tools applied to simulate some conditions producing glycolytic oscillations in e. coli cells. U.P.B. Sci. Bull. Series B - Chemie. 2018; 80(2): 27-38. http://www.scientificbulletin.upb.ro/.
- Maria G, Mihalachi M, Gijiu CL. In silico optimization of a bioreactor with an E. coli culture for tryptophan production by using a structured model coupling the oscillating glycolysis and tryptophan synthesis. Chemical Eng. Res. and Design. 2018; 135: 207-221. HTTPS://doi.org/10.1016/j.cherd.2018.05.011.
- Atkinson MR, Savageau MA, Myers JT, Ninfa AJ. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell. 2003 May 30;113(5):597-607. doi: 10.1016/s0092-8674(03)00346-5. PMID: 12787501.
- Salis H, Kaznessis Y. Numerical simulation of stochastic gene circuits. Computers &. Chemical Engineering. 2005; 29: 577-588.
- Klipp E, Liebermeister W, Wierling C, Kowald A, Lehrach H, Herwig R. Systems biology. A textbook, Wiley-VCH, Weinheim. 2009.
- Kaznessis YN. Multi-scale models for gene network engineering. Chemical Engineering Science. 2006; 61: 940-953.
- Klipp E, Nordlander B, Krüger R, Gennemark P, Hohmann S. Integrative model of the response of yeast to osmotic shock. Nat Biotechnol. 2005 Aug;23(8):975-82. doi: 10.1038/nbt1114. Epub 2005 Jul 17. Erratum in: Nat Biotechnol. 2006 Oct;24(10):1293. PMID: 16025103.
- Klipp E. Timing matters. FEBS Lett. 2009 Dec 17;583(24):4013-8. doi: 10.1016/j.febslet.2009.11.065. PMID: 19941864.
- Chen MT, Weiss R. Artificial cell-cell communication in yeast Saccharomyces cerevisiae using signaling elements from Arabidopsis thaliana. Nat Biotechnol. 2005 Dec;23(12):1551-5. doi: 10.1038/nbt1162. Epub 2005 Nov 20. PMID: 16299520.
- Tian T, Burrage K. Stochastic models for regulatory networks of the genetic toggle switch. Proc Natl Acad Sci U S A. 2006 May 30;103(22):8372-7. doi: 10.1073/pnas.0507818103. Epub 2006 May 19. PMID: 16714385; PMCID: PMC1482501.
- Tomshine J, Kaznessis YN. Optimization of a stochastically simulated gene network model via simulated annealing. Biophys J. 2006 Nov 1;91(9):3196-205. doi: 10.1529/biophysj.106.083485. Epub 2006 Aug 18. PMID: 16920827; PMCID: PMC1614480.
- Zhu R, Ribeiro AS, Salahub D, Kauffman SA. Studying genetic regulatory networks at the molecular level: delayed reaction stochastic models. J Theor Biol. 2007 Jun 21;246(4):725-45. doi: 10.1016/j.jtbi.2007.01.021. Epub 2007 Feb 6. PMID: 17350653.
- Xu Z, Zheng P, Sun J, Ma Y. ReacKnock: identifying reaction deletion strategies for microbial strain optimization based on genome-scale metabolic network. PLoS One. 2013 Dec 11;8(12):e72150. doi: 10.1371/journal.pone.0072150. PMID: 24348984; PMCID: PMC3859475.
- Xu Z, Sun X, Yu S. Genome-scale analysis to the impact of gene deletion on the metabolism of E. coli: constraint-based simulation approach. BMC Bioinformatics. 2009 Jan 30;10 Suppl 1(Suppl 1):S62. doi: 10.1186/1471-2105-10-S1-S62. PMID: 19208166; PMCID: PMC2648778.
- Xu Z, Sun J, Wu Q, Zhu D. Find_tfSBP: find thermodynamics-feasible and smallest balanced pathways with high yield from large-scale metabolic networks. Sci Rep. 2017 Dec 11;7(1):17334. doi: 10.1038/s41598-017-17552-2. PMID: 29229946; PMCID: PMC5725421.
- Gilbert D, Heiner M, Jayaweera Y, Rohr C. Towards dynamic genome-scale models. Briefings in Bioinformatics. 2017; 1-14. doi: 10.1093/bib/bbx096
- Maria G. Application of (bio) chemical engineering principles and lumping analysis in modelling the living systems, Current Trends in Biomedical Engineering & Biosciences, 1(4), (Juniper publ, Irvine, CA, USA). 2017C. CTBEB.MS.ID.555566.
- Yang X, Mao Z, Huang J, Wang R, Dong H, Zhang Y, Ma H. The necessity of considering enzymes as compartments 1 in constraint-based genome-scale metabolic models, BioRxiv - The preprint server for biology. Cold Spring Harbor Lab (USA). 2022. https://doi.org/10.1101/2022.12.14.520512;
- Sotiropoulos V, Kaznessis YN. Synthetic tetracycline-inducible regulatory networks: computer-aided design of dynamic phenotypes. BMC Syst Biol. 2007 Jan 9;1:7. doi: 10.1186/1752-0509-1-7. PMID: 17408514; PMCID: PMC1885862.
- Hatzimanikatis V, Floudas CA, Bailey JE. Analysis and design of metabolic reaction networks via mixed?integer linear optimization. AIChE Jl. 1996; 42(5): 1277-1292.
- Maria G. Extended repression mechanisms in modelling bistable genetic switches of adjustable characteristics within a variable cell volume modelling framework. Chemical & Biochemical Engineering Quarterly. 2014; 28 (1): 35-51.
- Maria G. Application of lumping analysis in modelling the living systems -A trade-off between simplicity and model quality. Chemical and Biochemical Engineering Quarterly. 2006; 20: 353-373.
- Maria G. Modelling bistable genetic regulatory circuits under variable volume framework. Chemical and Biochemical Engineering Quarterly. 2007; 21: 417-434.
- Maria G. Building-up lumped models for a bistable genetic regulatory circuit under whole-cell modelling framework. Asia-Pacific Journal of Chemical Engineering. 2009; 4: 916-928. DOI:10.1002/apj.297.
- Maria G, Luta I. Structured cell simulator coupled with a fluidized bed bioreactor model to predict the adaptive mercury uptake by E. coli cells. Computers & Chemical Engineering. 2013; 58: 98-115. DOI: 10.1016/j.compchemeng.2013.06.004.
- Maria G. A whole-cell model to simulate the mercuric ion reduction by E. coli under stationary and perturbed conditions. Chemical and Biochemical Engineering Quarterly. 2009; 23 (3): 323-341.
- Maria G. A dynamic model to simulate the genetic regulatory circuit controlling the mercury ion uptake by E. coli cells. Revista de Chimie(Bucharest). 2010; 61(2): 172-186.
- Maria G, Luta I, Maria C. Model-based sensitivity analysis of a fluidized-bed bioreactor for mercury uptake by immobilised Pseudomonas putida cells. Chemical Papers. 2013; 67 (11): 1364-1375. DOI: 10.2478/s11696-013-0403-z.
- Guantes R, Poyatos JF. Dynamical principles of two-component genetic oscillators. PLoS Comput Biol. 2006 Mar;2(3):e30. doi: 10.1371/journal.pcbi.0020030. Epub 2006 Mar 31. PMID: 16604190; PMCID: PMC1420664.
- Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000 Jan 20;403(6767):335-8. doi: 10.1038/35002125. PMID: 10659856.
- Gonze D. Coupling oscillations and switches in genetic networks. Biosystems. 2010 Jan;99(1):60-9. doi: 10.1016/j.biosystems.2009.08.009. Epub 2009 Sep 6. PMID: 19735694.
- Bier M, Teusink B, Kholodenko BN, Westerhoff HV. Control analysis of glycolytic oscillations. Biophys Chem. 1996 Nov 29;62(1-3):15-24. doi: 10.1016/s0301-4622(96)02195-3. PMID: 8962468.
- Silva AS, Yunes JA. Conservation of glycolytic oscillations in Saccharomyces cerevisiae and human pancreatic beta-cells: a study of metabolic robustness. Genet Mol Res. 2006 Aug 31;5(3):525-35. PMID: 17117368.
- Termonia Y, Ross J. Oscillations and control features in glycolysis: numerical analysis of a comprehensive model. Proc Natl Acad Sci U S A. 1981 May;78(5):2952-6. doi: 10.1073/pnas.78.5.2952. PMID: 6454892; PMCID: PMC319477.
- Termonia Y, Ross J. Oscillations and control features in glycolysis: analysis of resonance effects. Proc Natl Acad Sci U S A. 1981 Jun;78(6):3563-6. doi: 10.1073/pnas.78.6.3563. PMID: 6455663; PMCID: PMC319610.
- Termonia Y, Ross J. Entrainment and resonance in glycolysis. Proc Natl Acad Sci U S A. 1982 May;79(9):2878-81. doi: 10.1073/pnas.79.9.2878. PMID: 6211676; PMCID: PMC346310.
- Heinzle E, Dunn IJ, Furukawa K, Tanner RD. Modelling of sustained oscillations observed in continuous culture of Saccharomyces Cerevisiae, In: Aarne, H. (Ed.), Proc. Modelling & Control of Biotechnical Process IFAC Conference. Helsinki (Finland), Aug. 1982; 17-19.
- Tyson JJ. Biochemical Oscillations, In: Fall, C.P., Marland, E.S., Wagner, J.M., Tyson, J.J. (Eds.), Computational Cell Biology. Springer Verlag, Berlin. 2002; 9.
- Franck UF. Feedback kinetics in physicochemical oscillators, Ber. Bunsenges. Phys. Chem. 1980; 84: 334-341.
- Maria G. A CCM-based modular and hybrid kinetic model to simulate the tryptophan synthesis in a fed-batch bioreactor using modified E. coli cells. Computers & Chemical Engineering. 2021; 153: 107450-107466. https://doi.org/10.1016/j.compchemeng.2021.107450
- Bhartiya S, Chaudhary N, Venkatesh KV, Doyle FJ 3rd. Multiple feedback loop design in the tryptophan regulatory network of Escherichia coli suggests a paradigm for robust regulation of processes in series. J R Soc Interface. 2006 Jun 22;3(8):383-91. doi: 10.1098/rsif.2005.0103. PMID: 16849267; PMCID: PMC1578758.
- Orth JD, Thiele I, Palsson BØ. What is flux balance analysis? Nat Biotechnol. 2010 Mar;28(3):245-8. doi: 10.1038/nbt.1614. PMID: 20212490; PMCID: PMC3108565.
- Schmid JW, Mauch K, Reuss M, Gilles ED, Kremling A. Metabolic design based on a coupled gene expression-metabolic network model of tryptophan production in Escherichia coli. Metab Eng. 2004 Oct;6(4):364-77. doi: 10.1016/j.ymben.2004.06.003. PMID: 15491865.
- Chen L. Rational metabolic engineering and systematic analysis of Escherichia coli for L-tryptophan bioproduction. PhD thesis, TU Hamburg. 2016.
- Chen M. Novel approaches for in vivo evolution, screening and characterization of enzymes for metabolic engineering of Escherichia coli as hyper L-tryptophan producer. PhD thesis, TU Hamburg. 2020.
- Chen L, Zeng AP. Rational design and metabolic analysis of Escherichia coli for effective production of L-tryptophan at high concentration. Appl Microbiol Biotechnol. 2017 Jan;101(2):559-568. doi: 10.1007/s00253-016-7772-5. Epub 2016 Sep 6. PMID: 27599980.
- Chen M, Chen L, Zeng AP. CRISPR/Cas9-facilitated engineering with growth-coupled and sensor-guided in vivo screening of enzyme variants for a more efficient chorismate pathway in E. coli. Metab Eng Commun. 2019 May 6;9:e00094. doi: 10.1016/j.mec.2019.e00094. PMID: 31193188; PMCID: PMC6520568.
- Minliang C, Chengwei M, Lin C, Zeng AP. Integrated laboratory evolution and rational engineering of GalP/Glk-dependent Escherichia coli for higher yield and productivity of L-tryptophan biosynthesis. Metab Eng Commun. 2021 Feb 13;12:e00167. doi: 10.1016/j.mec.2021.e00167. PMID: 33665119; PMCID: PMC7907822.
- Chen L, Chen M, Ma C, Zeng AP. Discovery of feed-forward regulation in L-tryptophan biosynthesis and its use in metabolic engineering of E. coli for efficient tryptophan bioproduction. Metab Eng. 2018 May;47:434-444. doi: 10.1016/j.ymben.2018.05.001. Epub 2018 May 5. PMID: 29733896.
- Xiu ZL, Zeng AP, Deckwer WD. Model analysis concerning the effects of growth rate and intracellular tryptophan level on the stability and dynamics of tryptophan biosynthesis in bacteria. Journal of Biotechnology. 1997; 58: 125-140.
- Xiu ZL, Chang ZY, Zeng AP. Nonlinear dynamics of regulation of bacterial trp operon: model analysis of integrated effects of repression, feedback inhibition, and attenuation. Biotechnol Prog. 2002 Jul-Aug;18(4):686-93. doi: 10.1021/bp020052n. PMID: 12153299.
- Mihalachi M, Maria G. Influence of PEP glycolytic precursor on tryptophan synthesis dynamics in E. coli cells, U.P.B. SCI. BULL., SERIES B - CHEMIE. 2019; 81(2): 29-36, http://www.scientificbulletin.upb.ro/.
- Maria G, Scoban AG. Optimal operating policy of a fluidized bed bioreactor used for mercury uptake from wastewaters by using immobilized P. putida cells, Current Trends in Biomedical Engineering & Biosciences. (Juniper publ, Irvine, CA, USA). 2017; 2(4):555594. DOI: 10.19080/CTBEB.2017.02.555594.
- Philippidis GP, Malmberg LH, Hu WS, Schottel JL. Effect of gene amplification on mercuric ion reduction activity of Escherichia coli. Appl Environ Microbiol. 1991 Dec;57(12):3558-64. doi: 10.1128/aem.57.12.3558-3564.1991. PMID: 1785930; PMCID: PMC184012.
- Philippidis GP, Schottel JL, Hu WS. Mathematical modelling and optimization of complex biocatalysis. A case study of mercuric reduction by Escherichia coli, Expression systems and processes for DNA Products. National Science Foundation Report ECE-8552670, University of Minnesota. 1991.
- Philippidis GP, Schottel JL, Hu WS. A model for mercuric ion reduction in recombinant Escherichia coli. Biotechnol Bioeng. 1991 Jan 5;37(1):47-54. doi: 10.1002/bit.260370108. PMID: 18597306.
- Barkay T, Miller SM, Summers AO. Bacterial mercury resistance from atoms to ecosystems. FEMS Microbiol Rev. 2003 Jun;27(2-3):355-84. doi: 10.1016/S0168-6445(03)00046-9. PMID: 12829275.
- Maria G. Comments on several review eBooks promoting a novel kinetic modelling framework of metabolic processes and of genetic regulatory circuits in living cells. Curr Trends in Biomedical Eng & Biosci. (Juniper publ, Irvine CA, USA). 2023; 21(2): 556057. DOI: 10.19080/CTBEB.2023.21.556057, 2023,
- Deckwer WD, Becker FU, Ledakowicz S, Wagner-Döbler I. Microbial removal of ionic mercury in a three-phase fluidized bed reactor. Environ Sci Technol. 2004 Mar 15;38(6):1858-65. doi: 10.1021/es0300517. PMID: 15074700.
- Wagner-Döbler I, von Canstein H, Li Y, Timmis K, Deckwer WD. Removal of mercury from chemical wastewater by microorganisms in technical scale. Env. Sci. & Technol. 2000; 34: 4628-4634.
- Leonhäuser J, Röhricht M, Wagner-Döbler I, Deckwer WD. Reaction engineering aspects of microbial mercury removal. Eng. Life Sci. 2006; 6: 139-148.
- Berne F, Cordonnier J. Industrial water treatment. Paris, Gulf Publishing Co. 1995.
- Ledakowicz S, Becker U, Deckwer WD. Development of mercury biotransformation process in fluidised-bed reactor with immobilized microorganisms, In: Wijffels RH, Buitelaar RM, Bucke C, Tramper J. (Eds.), Immoblized cells: Basics and applications. Elsevier, Amsterdam 1996.
- Moser A. Bioprocess technology - kinetics and reactors. Springer Verlag, Berlin. 1988.
- Trambouze P, Van Landeghem H, Wauquier JP. Chemical reactors: Design, engineering, operation. Paris: Edition Technip. 1988.
- Doraiswamy LK, Sharma MM. Heterogeneous reactions: Analysis, examples, and reactor design. New York: Wiley. 1984; 1-2.
- Doran PM. Bioprocess engineering principles. Elsevier, Amsterdam. 1995.
- Narasimhan B, Mallapragada SK, Peppas NA. Release kinetics, data interpretation. In: Mathiowitz, E. (Ed.), Encyclopedia of controlled drug delivery. New York: Wiley. 1999; 921-935.
- EcoCyc. Encyclopedia of Escherichia coli K-12 genes and metabolism, SRI Intl., The Institute for Genomic Research. Univ. of California at San Diego. 2005. http://ecocyc.org/
- Chassagnole C, Noisommit-Rizzi N, Schmid JW, Mauch K, Reuss M. Dynamic modeling of the central carbon metabolism of Escherichia coli. Biotechnol Bioeng. 2002 Jul 5;79(1):53-73. doi: 10.1002/bit.10288. PMID: 17590932.
- Costa RS, Machado D, Rocha I, Ferreira EC. Large scale dynamic model reconstruction for the central carbon metabolism of Escherichia coli, In: Omatu, S., et al. (Eds.): Distributed Computing, Artificial Intelligence, Bioinformatics, Soft Computing, and Ambient Assisted Living, Proc. IWANN conf., Salamanca (Spain), June 10-12, 2009, Part II, LNCS 5518. Springer-Verlag, Berlin. 2009; 1079-1083.
- Costa RS, Machado D, Rocha I, Ferreira EC. Hybrid dynamic modeling of Escherichia coli central metabolic network combining Michaelis-Menten and approximate kinetic equations. Biosystems. 2010 May;100(2):150-7. doi: 10.1016/j.biosystems.2010.03.001. Epub 2010 Mar 10. PMID: 20226228.
- Machado D, Zhuang KH, Sonnenschein N, Herrgård MJ. Editorial: Current Challenges in Modeling Cellular Metabolism. Front Bioeng Biotechnol. 2015 Nov 26;3:193. doi: 10.3389/fbioe.2015.00193. PMID: 26636080; PMCID: PMC4659907.
- Kiparissides A, Koutinas M, Kontoravdi C, Mantalaris A, Pistikopoulos EN. Closing the loop' in biological systems modeling - From the in silico to the in vitro, Automatica. 2011; 47: 1147-1155. doi:10.1016/j.automatica.2011.01.013.
- Whitham AG, Sparks RSJ. Pumice. Bulletin of Volcanology. 1986; 48: 209-223.
- Lambert DP. Ventilation criteria for IDMS facility, DOE contract DE-AC09-89SR18035 (Report WSRC-RP-96-0282), Westinghouse Savannah River Company. Aiken (USA). 1996.
- Shen L, Chen Z. Critical review of the impact of tortuosity on diffusion. Chem. Eng. Sci. 2007; 62: 3748-3755.
- Alvarez E, Cancela MA, Navaza JM, Taboas R. Mass transfer coefficients in batch and continuous regime in a bubble column, In: Proc. Intl. Conference on Distillation and Absorption (Baden-Baden, Germany, Sept. 2002), Düsseldorf: GVC - VDI Society of Chemical and Process Engineering. 2002.
- Laurent M, Charvin G, Guespin-Michel J. Bistability and hysteresis in epigenetic regulation of the lactose operon. Since Delbrück, a long series of ignored models. Cell Mol Biol (Noisy-le-grand). 2005 Dec 14;51(7):583-94. PMID: 16359608.
- Morgan JJ, Surovtsev IV, Lindahl PA. A framework for whole-cell mathematical modeling. J Theor Biol. 2004 Dec 21;231(4):581-96. doi: 10.1016/j.jtbi.2004.07.014. PMID: 15488535.
- Wang X, Li Y, Xu X, Wang YH. Toward a system-level understanding of microRNA pathway via mathematical modeling. Biosystems. 2010 Apr;100(1):31-8. doi: 10.1016/j.biosystems.2009.12.005. Epub 2009 Dec 28. PMID: 20005918.
- Trun NJ, Gottesman S. On the bacterial cell cycle: Escherichia coli mutants with altered ploidy. Genes Dev. 1990 Dec;4(12A):2036-47. doi: 10.1101/gad.4.12a.2036. PMID: 2176633.
- Kubitschek HE. Cell volume increase in Escherichia coli after shifts to richer media. J Bacteriol. 1990 Jan;172(1):94-101. doi: 10.1128/jb.172.1.94-101.1990. PMID: 2403552; PMCID: PMC208405.
- Mackay D. Multimedia environmental models - The fugacity approach, Boca Raton. Lewis Publ. 2001.
- Rassis D, Nussinovitch A, Saguy IS. Collapse, shrinkage and structural changes in dried alginate gels containing fillers. Food Hydrocolloids. 2002; 16(2): 139-151.
- Moulijn JA, Makkee M, van Diepen A. Chemical process technology. New York, Wiley. 2001; ISBN 0-471-63009-8.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
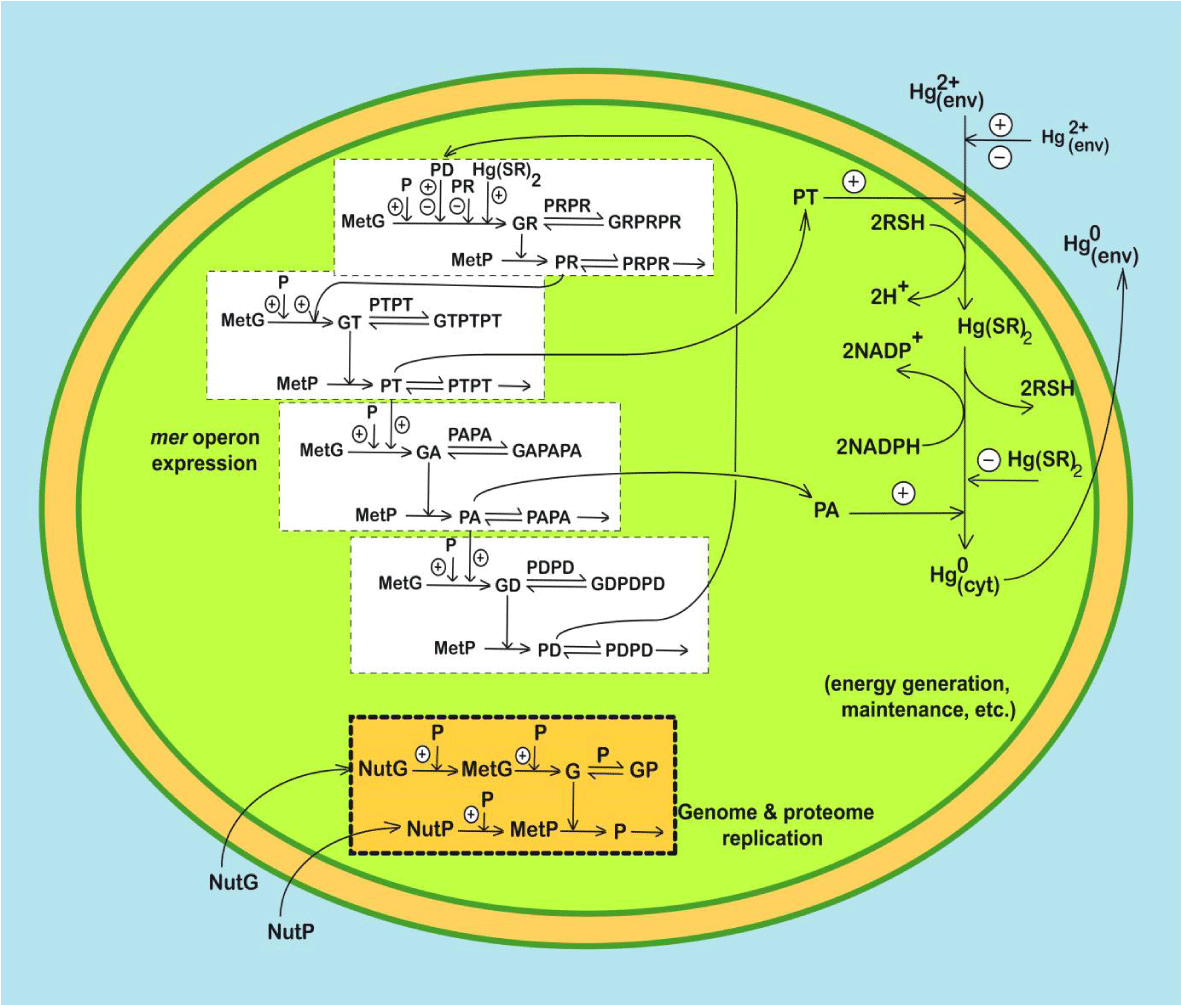
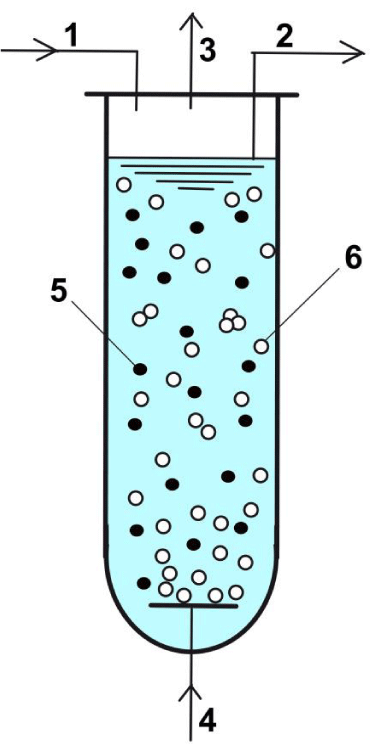

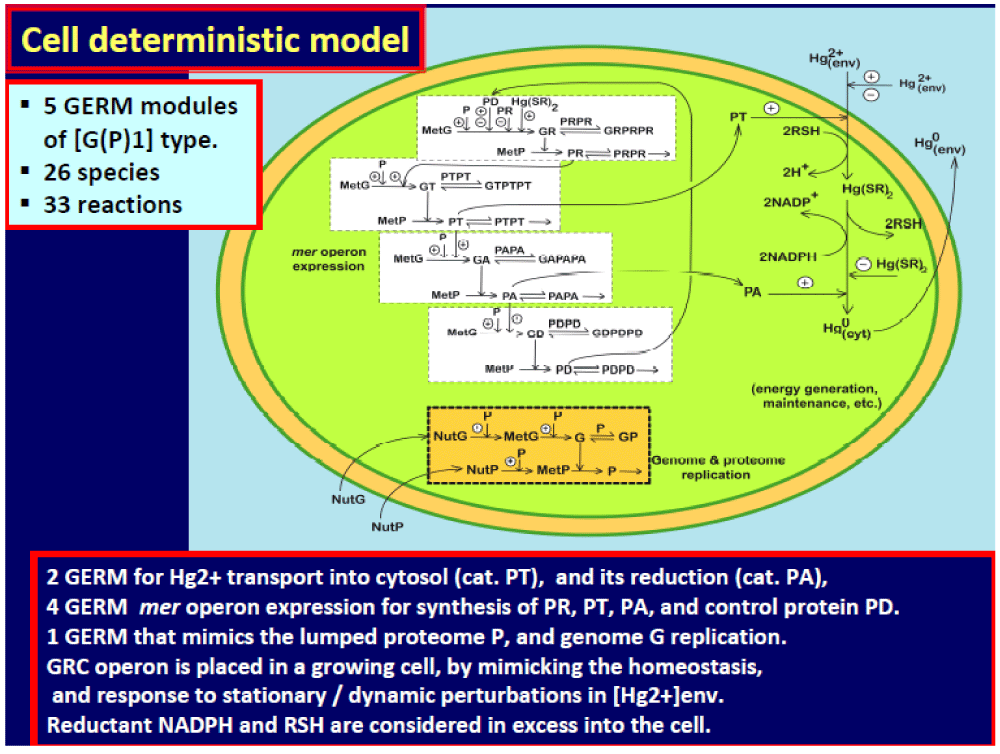

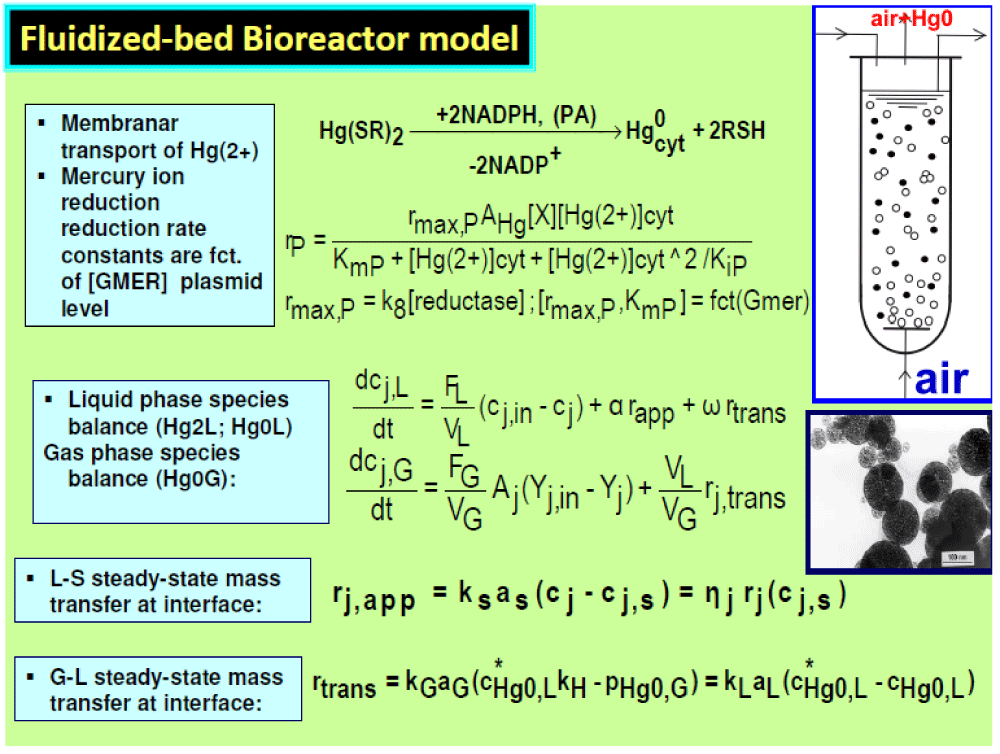
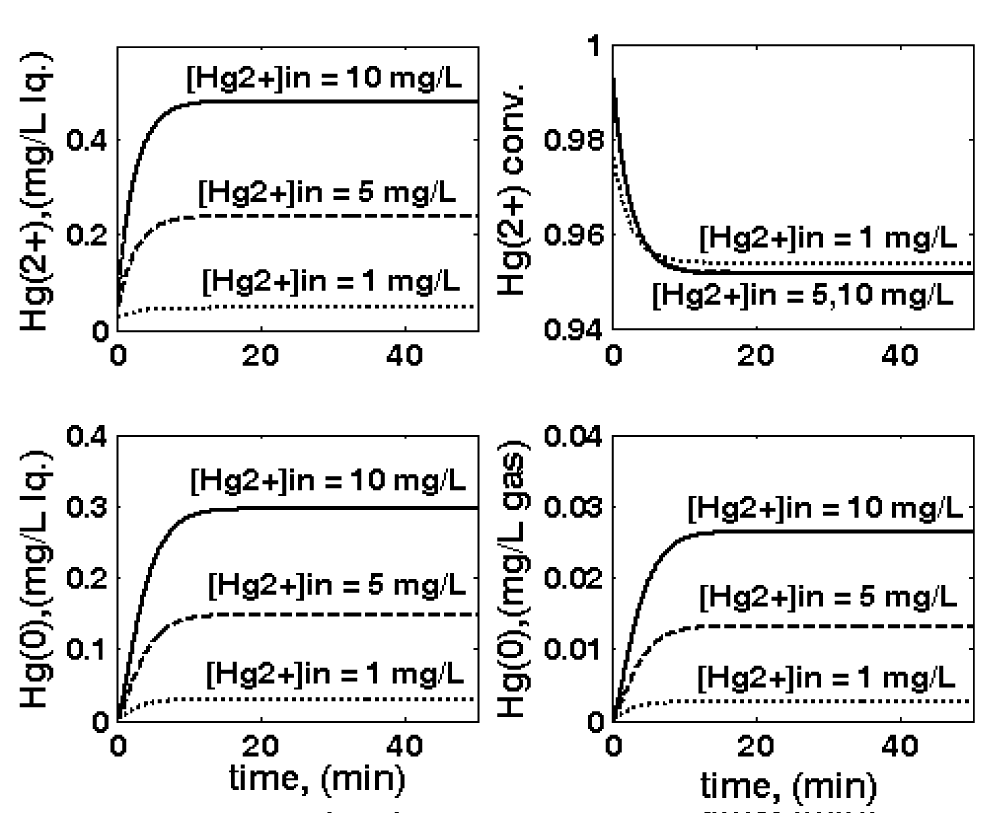
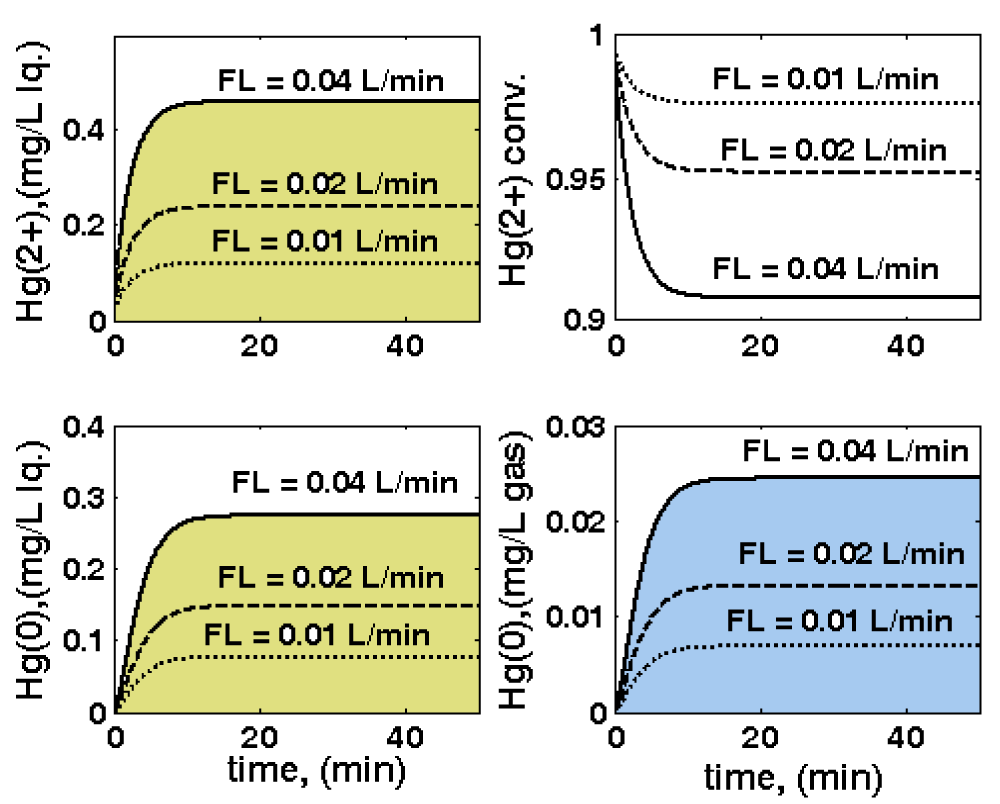
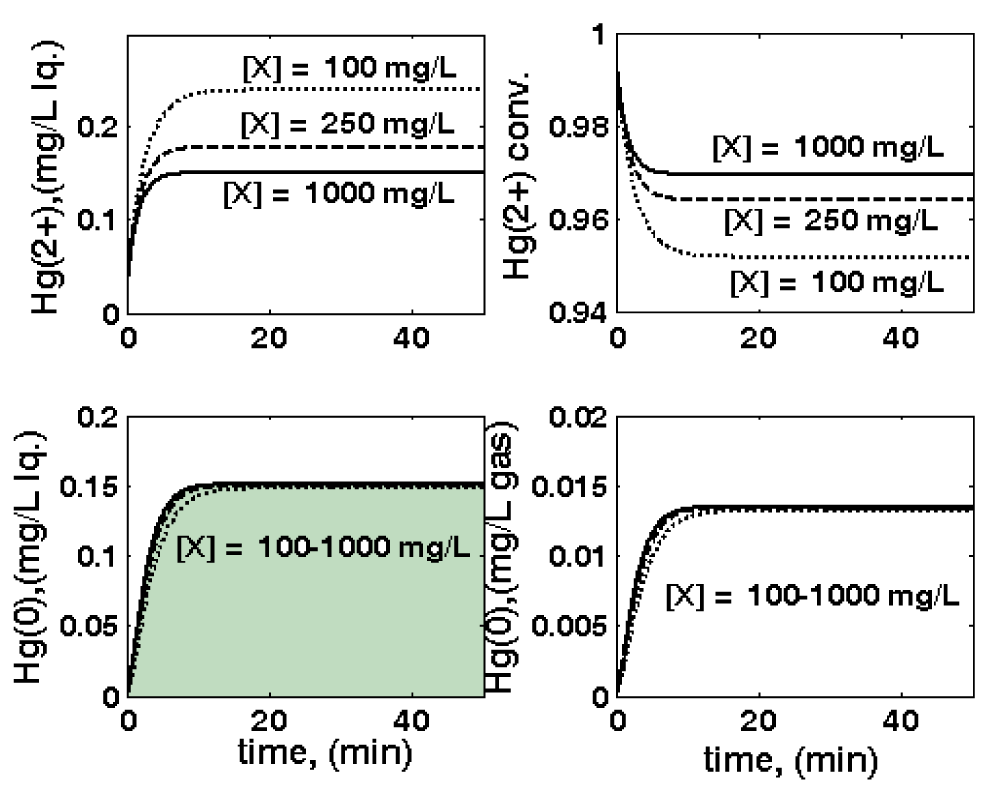
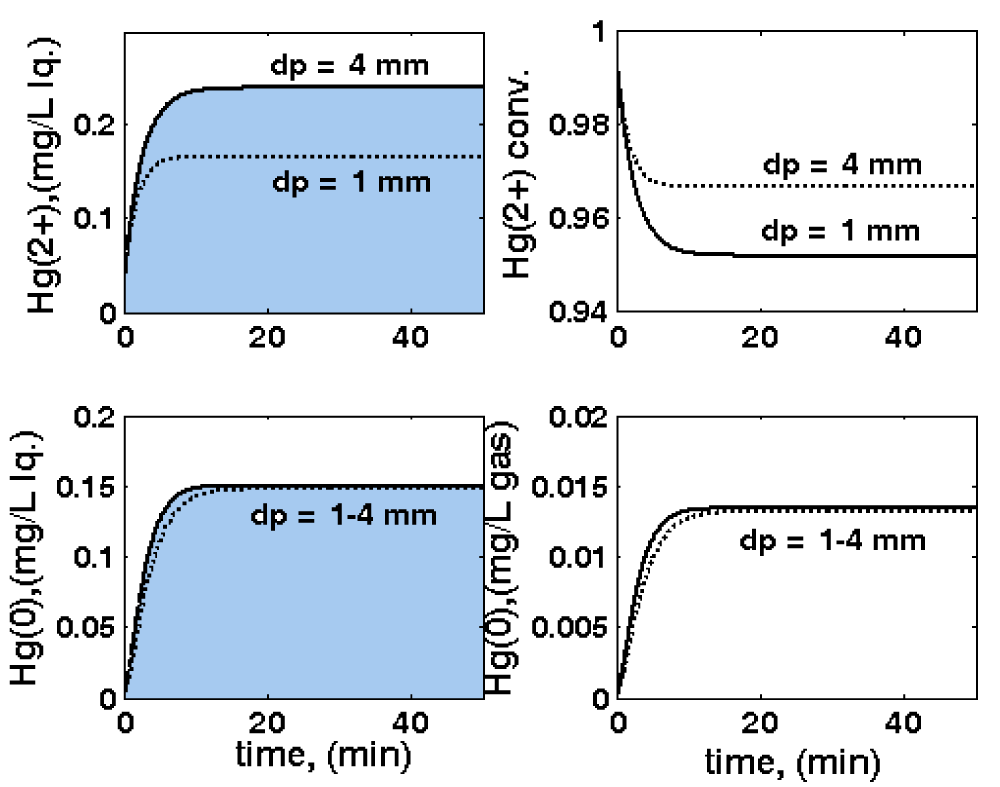
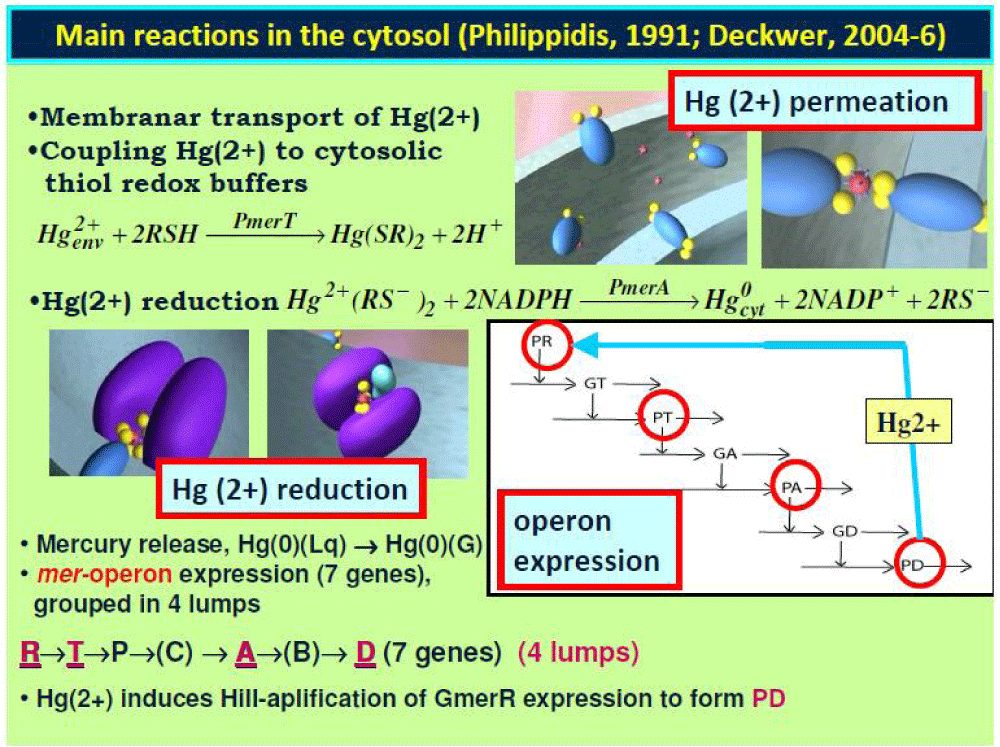

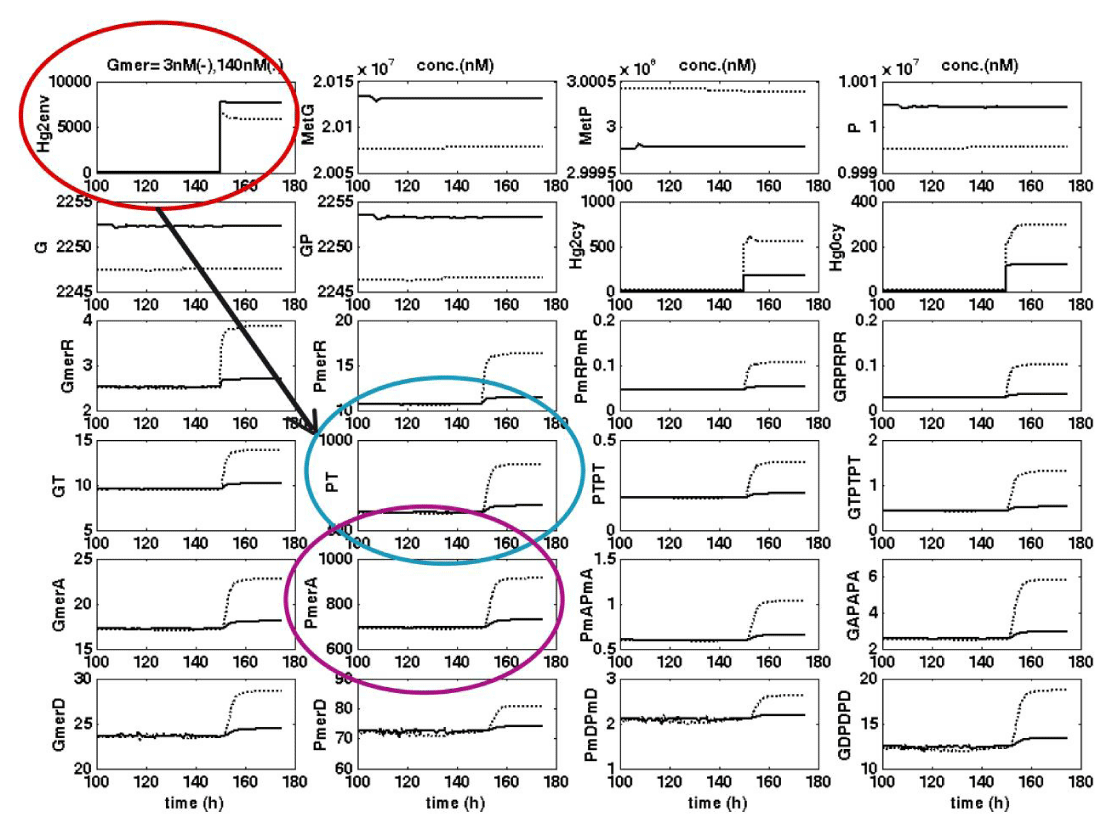
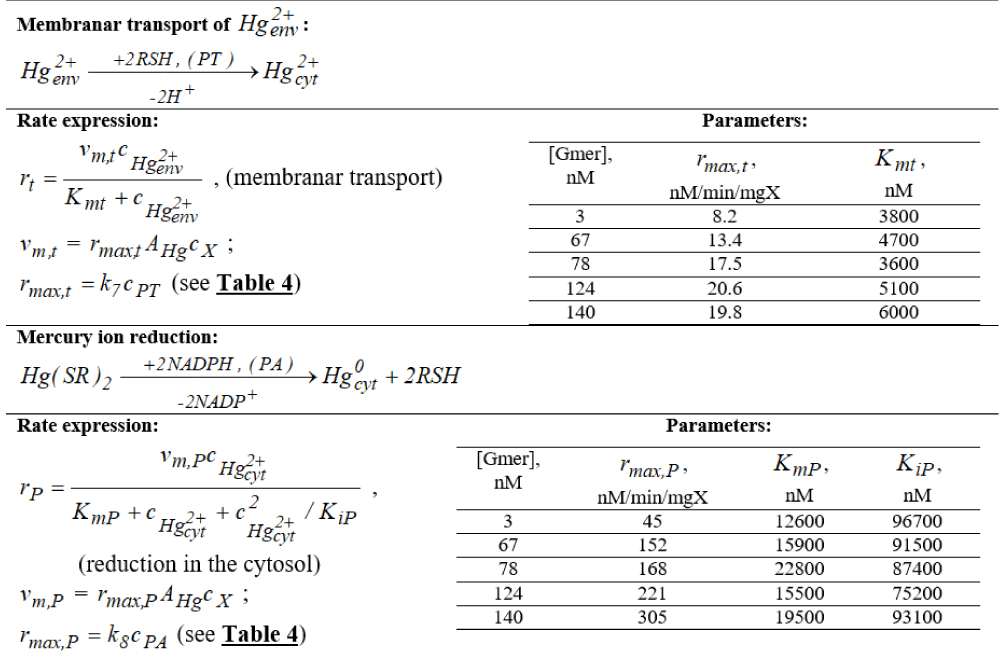

.gif)
.gif)
.gif)
.gif)
.gif)



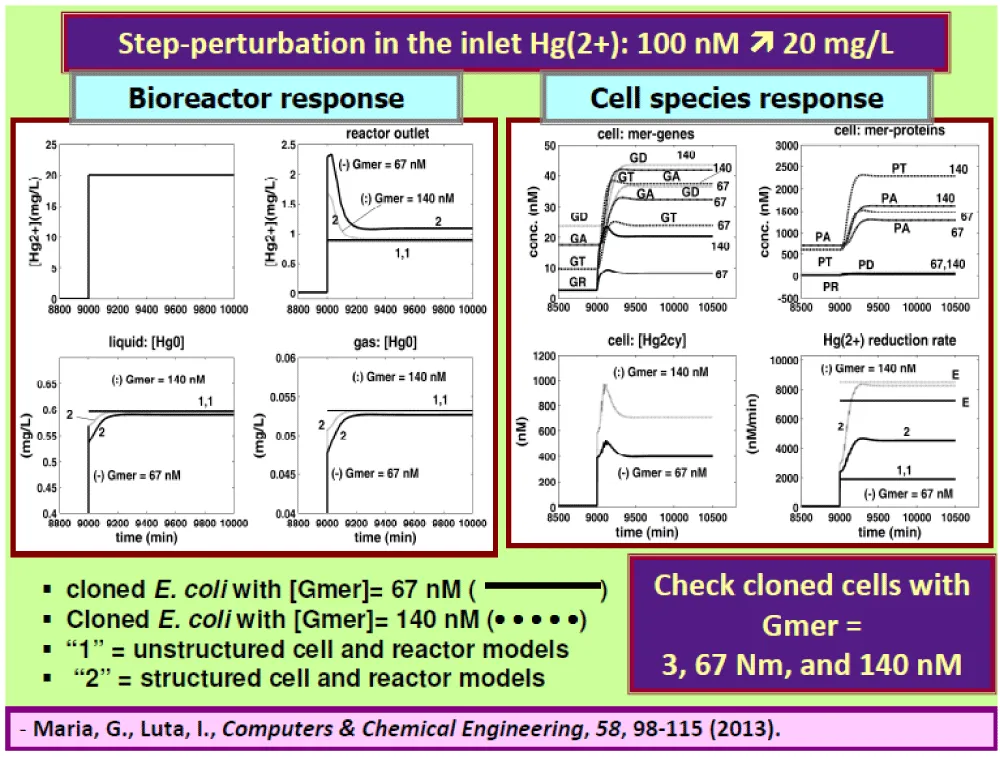
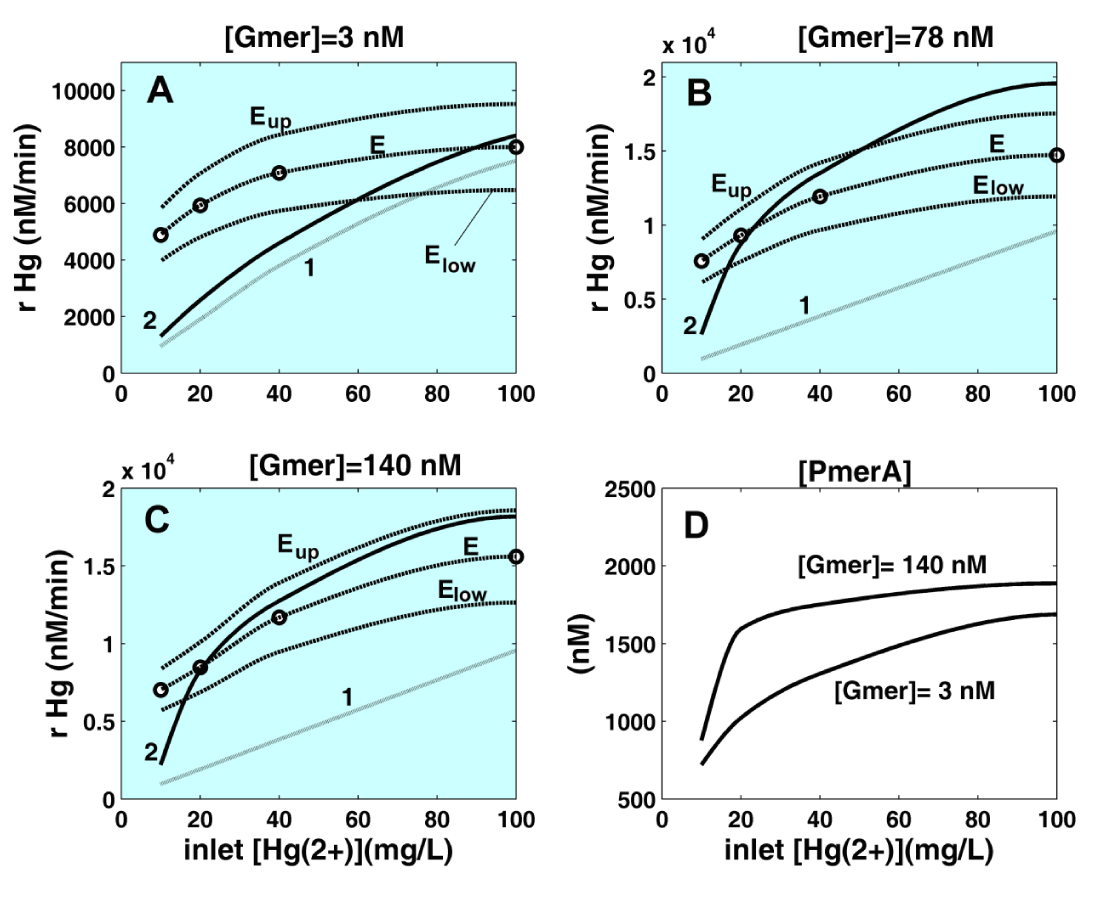


 Save to Mendeley
Save to Mendeley
