The Influence of Temperature Conditions on the Bioproductivity of Waters and Tuna Fishing in the South China Sea

The main abiotic factor influencing the formation and variability of the bioproductivity characteristics of the waters of the South China Sea (SCS), as well as the distribution and migration of tuna, is the water temperature. The impact of other abiotic factors is less significant. The Scientific Research Institute of Marine Fisheries of Vietnam has carried out many years of work to assess the influence of various characteristics of water temperature on changes in bioproductivity parameters, but the patterns of their interannual variability have not been identified. Also, the problem of constructing fish catch models depending on the determining factors remained completely unexplored, and even more so, the development of a forecasting method, which is extremely important when planning a fishery. In this paper, for the first time, an attempt is made to identify the role of various characteristics of water temperature on the parameters of bioproductivity of waters of the South China Sea. A statistical model of tuna catch has been created depending on economic and oceanological factors.

Introduction

The South China Sea is characterized by the exceptionally high biological productivity of its waters, which contributes to the formation of large commercial stocks of pelagic fish (tuna, southern herring, sardines, mackerel, humpback, sea eel, etc.), and the proximity of the coastal zone and the rapid growth of the economy and population contribute to the increase of fishing efforts here. But tuna fishing is of particular importance, as it is extremely valuable in terms of food and is in unlimited demand among consumers. Tuna fishing occupies the 1st place in the structure of exports of marine fish products from Vietnam to more than 60 countries of the world and in 2015 it amounted to more than 408 million USD. However, intensive tuna fishing in Vietnam began to develop only from the beginning of this century, when the Government of the country set a strategic task to dramatically strengthen fishing by accelerating the construction of new more powerful fishing vessels, reorganizing coastal infrastructure, applying new technologies in the processing of fish products, expanding cooperation with other countries in the region and in the world, etc. This became possible as a result of the rapid growth of Vietnam’s gross domestic product, which has grown 6 times in 15 years.

It is very important to note that there is a possibility of increasing fish catch without the threat of undermining the fishing stock, which, according to the Scientific Research Institute of Marine Fisheries of Vietnam, is estimated at 662-670 thousand tons. At the same time, the total allowable catch is about 233 thousand tons, and currently, about 80 thousand tons per year are mined. The main abiotic factor influencing the formation and variability of the bioproductivity characteristics of the waters of the South China Sea (SCS), as well as the distribution and migration of tuna, is the water temperature. The impact of other abiotic factors is less significant. Although the Scientific Research Institute of Marine Fisheries of Vietnam has carried out many years of work to assess the influence of various characteristics of water temperature on changes in bioproductivity parameters, however, patterns of their interannual variability have not been identified. The problem of constructing fish catch models depending on the determining factors and, moreover, the development of a forecasting method, which is extremely important when planning a fishery, is completely unexplored. The purpose of this work is to identify the impact of various characteristics of water temperature on the parameters of bioproductivity of waters of the South China Sea, to build a statistical model of tuna catch depending on economic and oceanological factors, and to develop a methodology for long-term forecasting of tuna catch. To achieve this goal, the following tasks were solved:

- the peculiarities of the distribution and formation of the commercial tuna stock in the South China Sea are revealed;

- the analysis of quantitative relationships of the influence of various temperature characteristics on the parameters of bioproductivity of the South China Sea was performed;

- the spatial and temporal patterns of the distribution of the depth of the critical isotherm of 24 oC are revealed;

- a statistical model of annual tuna catch values has been created depending on economic and oceanological factors;

- A methodology has been developed for long-term forecasting of annual tuna catch values.

The basis for the work was:

- Data on bioproductivity characteristics, tuna catch, and economic indicators, which are provided by the Scientific Research Institute of Marine Fisheries of Vietnam, the Department of Fisheries and Conservation of Biological Resources of Vietnam, and the Department of General Statistics of Vietnam. For the first time, a unique time series of the total tuna catch by Vietnamese fishing vessels in the South China Sea for the period 2000-2015 is used in statistical calculations. The following water temperature characteristics were used in the work, which were selected from the reanalysis archives that are freely available on the Internet:

- monthly average data on ocean surface temperature in the nodes of the 2 × 2 ° latitude and longitude grid from the NOAA NCDC ERST global archive (National Oceanic and Atmospheric Administration National Climatic Data Center Extended Reconstructed Sea Surface Temperature);

- monthly average data on deep-sea temperature in the nodes of the latitude-longitude grid 0.5 × 0.5° from the global archive CARTON-GIESE SODA (Simple Ocean Data Assimilation). To solve the tasks set, a wide range of standard methods of one-dimensional and multidimensional statistical analysis contained in modern packages of applied statistical programs (PPMS), including parametric and nonparametric correlation analysis, paired and multiple regression models, factor analysis, interpolation methods in the construction of maps, etc.

For the first time, a biological and commercial generalization of the three main tuna species (yellowfin, big-eyed, and striped) that make up the commercial stock of the South China Sea is presented.

An assessment of the influence of 18 different water temperature indicators on a complex of 6 parameters of the bioproductivity of the waters of the South China Sea was carried out. It is shown that the maximum correlation of all bioproductivity parameters is noted for the isotherm depth of 24 oC, which varies from -0.70 to -0.94. The second most important is the depth of the isotherm of 20 ° C, and the third is the temperature of the sea surface. With all these parameters, the correlation turns out to be negative. This means that with the deepening of isotherms 20 and 24 oC and an increase in sea surface temperature, all the characteristics of bioproductivity should decrease.

For the first time, using factor analysis, the zoning of the South China Sea fishing area was performed according to the nature of the interannual fluctuations of the isotherm of 24 oC for the period 1980-2008. 5 quasi-homogeneous regions have been identified. Mainly random interannual fluctuations are observed in the time course of common factors. One can only note the presence of a weak 6- to 8-year cycle, which is also manifested in tuna stocks in the world’s oceans.

For the first time, a statistical model of interannual tuna catch values has been constructed depending on economic (number of fishing vessels) and oceanological (sea surface temperature in the nodes of the grid area) factors, which describes 95% of the variance of the initial series and has a small standard error.

For the first time, a method for long-term forecasting of annual tuna catch values based on extrapolation of a time series with its approximation by a polynomial model and a second-order autoregressive model has been proposed. Checking the results on independent data for 2015 showed a good match.

The theoretical significance lies in the fact that the contribution of economic and oceanological factors to the statistical model of tuna fishing has been revealed. The economic factor (the number of fishing vessels) is the main one, accounting for 75% of the variance of the initial series. The high efficiency of the autoregressive model for predicting fish catch with a lead time of 1 year has been revealed. The discrepancy between the actual and estimated data for 2015 amounted to 1,470 tons, or 2%. The practical significance lies in the fact that the results obtained will be implemented in the activities of the Ministry of Agriculture of Vietnam and will be used in the planning of fishing and rational exploitation of tuna resources. The validity and reliability of the results of the work are confirmed by high-quality initial information used in modeling and forecasting, competent application of modern methods of one-dimensional and multidimensional statistical analysis, and comparison of the results obtained with actual data.

Materials and methods of research

The basis for the work was

- Data on bioproductivity characteristics, tuna catch, and economic indicators provided by the staff of the Scientific Research Institute of Marine Fisheries of Vietnam Dinh Van Uy, Doan Van Vo, Bui Thanh Hung, etc., the Department of Fisheries and Conservation of Biological Resources of Vietnam and the Department of General Statistics of Vietnam.

- The objects of the study were yellowfin (Thunnus albacares), big-eyed (Th. obesus), and striped (Katsuwonus pelamis) tuna, which are the main object of fishing in the offshore waters of the central part of the South China Sea. For the first time, a unique time series of the total tuna catch by Vietnamese fishing vessels in the South China Sea for the period 2000-2015 is used in statistical calculations. The study area was limited by the following latitude and longitude zones: 6-17o S.S., 107-117o V.D. It is in this area, located mainly in the central part of the South China Sea, that Vietnamese vessels fish.

The following water temperature characteristics were used in the work, which were selected from the reanalysis archives that are freely available on the Internet:

- monthly average data on ocean surface temperature in the nodes of the 2 × 2 ° latitude and longitude grid from the NOAA NCDC ERST global archive (National Oceanic and Atmospheric Administration National Climatic Data Center Extended Reconstructed Sea Surface Temperature);

- monthly average data on deep-sea temperature in the nodes of the latitude-longitude grid 0.5 × 0.5° from the global archive CARTON-GIESE SODA (Simple Ocean Data Assimilation).

Statistical methods for analyzing the data used in the work. To solve the tasks set, a wide range of standard methods of one-dimensional and multidimensional statistical analysis contained in modern packages of applied statistical programs (PPMS) was used, including parametric and nonparametric correlation analysis, paired and multiple regression models, factor analysis, interpolation methods for constructing maps, etc.

Let’s briefly consider only the basic methods of data processing and analysis used in the work.

Identification and analysis of trends.

In general, the interannual variability of any characteristic can be represented as the following decomposition [1].

X(t) = T(t) + C(t) + E(t), (1)

where T(t) is the trend component, C(t) is the component characterizing cyclic fluctuations time series, and E(t) is the residual part characterizing irregular fluctuations. Obviously, the sum of the first two terms in decomposition (1) can be considered as a deterministic part of a stochastic series, while the third term is a random part. In decomposition (1), the trend component will be understood as a certain slow change in the process with a period exceeding the length of the initial implementation [1]. It follows that the very existence of a trend is completely determined by the length of the series. Whens its length changes, the trend may appear, disappear, or change its intensity and shape. In essence, the trend shows which way (up or down) the process is developing over time. But at the same time, it cannot form cycles, which, as can be seen from the decomposition (1), are described by the second term.

Note that there is still some confusion about the concept of a trend. In a number of works [2,3], the trend is identified with the trend, which is usually understood as the main pattern in the development of a random process. Therefore, unlike a trend, the trend of a time series can form cycles. There is also an opinion [4] that a trend should be understood as a deterministic component of a time series. In addition, in some cases, a trend is understood to be the longest-period component of a time series.

Obviously, in some cases, in addition to the main (main) trend, it is advisable to highlight local trends. The main trend is for the entire time series. If the series is divided into separate characteristic segments that differ from each other in the direction of time fluctuations, then for each of them you can build your own local trends. Naturally, highlighting local trends makes sense only for long-time series. Fishing characteristics do not always correspond to this condition.

It is shown in [5] that several types of trend are possible: by the average value, when the sample average changes linearly or non-linearly over time; trend by variance, when the range of fluctuations changes, trend by average and variance at the same time, and trend by the autocorrelation function, when it depends not only on the time shift, but also and from the beginning of the countdown. The trend in the average value is most common, including in fishing characteristics. It can be linear or nonlinear in form and is usually approximated by polynomial approximations. A linear trend can be represented as:

T(t) = a₀ + a₁t, (2)

where t is the time. In this case, the free term a₀ shows the conditional value of the series X(t) at t = 0. The angular coefficient (regression coefficient) a₂ is the magnitude of the trend (Tr), meaning the rate of increase (decrease) of the characteristic in question per unit of time. The nonlinear trend is expressed by a polynomial of the second degree:

T(t) = a₀ + a₁t + a₂t₂, (3)

The a₂ coefficient shows the acceleration (deceleration) of the rate of change of the considered characteristic over time squared, i.e. the parabolic shape of the trend corresponds to an accelerated or delayed change in the values of the series with constant acceleration. If a₂ < 0 and a₁ > 0, then the quadratic parabola has a maximum, if a₂ > 0 and a₁ < 0 – a minimum. To find the extremum, the first derivative of the parabola with respect to t is equated to 0 and the equation with respect to t is solved.

The numerical values of the coefficients in these formulas are determined by the least squares method. Of course, there are other ways to approximate the trend. When assessing a trend, it is most important to assess its significance, i.e. how significant its contribution to the variability of a random process is. The Student’s criterion is used for this purpose. Thus, when assessing the significance of a linear trend, a null hypothesis is recorded with respect to the regression coefficient a₁ and the correlation coefficient between the time series and the trend component r(X,T):

H₀ : |a₁| = 0, H₀ : |r_(X,T)| = 0, (4)

To test these hypotheses, a Student’s sample criterion is calculated, and it can be shown that tr = ta1. This makes it easier to assess the significance of the trend. The sample value of the Student’s statistics is calculated as:

$t=\frac{\left|r\right|\sqrt{n-2}}{\sqrt{1-r^2}}\text{ (5)}$

A trend is considered significant if the Student’s criterion scores exceed its critical value at a given level of significance, i.e.

t > t_cr(α, ν = n–2), (6)

The significance of the trend can be estimated approximately by the critical value of the correlation coefficient. For sufficiently long time series and the significance level α = 0.05, we have $r_{кр}\approx \frac{2}{\sqrt{n+2}}$ [6]. If r_(X,T) > r _kr, then the trend can be considered significant. In modern PPTs, the significance of the trend can be determined directly by evaluating the p-level coefficient a1.

When assessing the significance of a nonlinear trend, the correlation ratio η is calculated, and then the null hypothesis is tested as a correlation coefficient. By the value of the correlation coefficient and the correlation ratio, it is easy to determine the coefficient of determination, which shows the contribution of the trend to the description of the variance of the response function. It is determined in linear and nonlinear versions using the same formula R² = σ²Tr /σ²y, where the numerator is the variance of the trend, and the denominator is the variance of the original series. Note that the coefficient of determination can also be used to assess the significance of the trend. For sufficiently long time series and the significance level α = 0.05, we have R2kr ≈ 4/(n+2) [1].

Another important characteristic of the trend is its value Tr, defined in the linear case as:

$Tr=\frac{(a_0+a_1{t}_n)-(a_0+a_1{t}_1)}{n}=\frac{a_1(n-1)}{n}\approx a_1,\text{ (7)}$

where n is the length of the series. It can be seen from this that the magnitude of the linear trend is determined by the regression coefficient. Similarly, for a nonlinear trend, its first and last values are calculated using the formula (3) and then the difference is divided by the length of the interval. As a result, we get the value of the trend per unit of time. However, at the same time, Tr ≠ a1. It should be borne in mind that the coefficient of determination calculated in this way for a nonlinear trend is higher than for a linear trend.

At the same time, the greater the “steepness” of the trend, the greater the difference between linear and nonlinear trends.

So, the coefficient of determination and the magnitude of the trend comprehensively characterize the behavior of the trend. However, it must be remembered that the above procedure for estimating trends is parametric, the effectiveness of which significantly depends on how accurately the initial series is close to the normal distribution and on its length. Indeed, for long series, even if the initial series is not normal, trend estimation can be carried out in the manner discussed above quite accurately. For short series, especially when the distribution of the initial data is unknown, the effectiveness of trend estimation using formulas (2) − (7) decreases. In this case, nonparametric Spearman or Kendall rank correlation coefficients can be used to estimate the coefficient of determination, followed by an approximate assessment of significance according to the Student’s criterion [6].

Multiple regression analysis

As a rule, fishing characteristics are determined by a large set of factors, the combined effect of which may have different effects on the process under study. Therefore, there is a need to study the effects of various causes simultaneously. This problem is solved using the classical method of data analysis – multiple (multifactorial) regression analysis.

The method of multiple regression analysis is used in almost all applied sciences as the most universal method of analyzing source data, and hundreds of modifications of this method have been developed to solve specific problems. Due to its flexibility, simplicity, and theoretical sophistication, it is an integral part of many other methods of multidimensional statistical analysis. In general, the multiple linear regression (MLR) model can be represented as follows:

$y=b_0+{\displaystyle \sum _{j=1}^m{b}_j{x}_j}+{\epsilon }_j\text{ (8)}$

where m is the number of variables x_j in the model, ε_j is the vector of residuals (errors) that are not described by the MLR equation. The regression coefficients b_j are calculated based on the least squares method.

To build an effective MLR model, the following conditions must be met:

– MLR errors must have a zero mean;

– homoscedasticity of regression residuals, i.e. their variance should be constant;

– errors should be independent (uncorrelated) with factors and response function;

– there should be no multicollinearity between independent variables;

– preferably, but not necessarily, a normal distribution of residues.

The mathematical description of MLR is contained in many works [7,8,9,10], so here we will limit ourselves to a brief description of only those aspects that are necessary to understand the calculations performed. The following parameters are used to evaluate the quality of the MLR model:

1. A multiple linear correlation coefficient, which is an analogue of the usual paired correlation coefficient, characterizing the measure of the linear relationship between the actual and calculated values of the response function according to the MLR equation, i.e.

$r=\frac{1}{n{\sigma }_y{\sigma }_{y(x)}}{\displaystyle \sum _{i=1}^n(y_i-\overline{y})({\tilde{y}}_i-\overline{y})}\text{ (9)}$

where ${\tilde{y}}_i$ the response values are calculated according to the MLR model, σ_y(x) is the standard deviation of the values ${\tilde{y}}_i$ .

The value of R varies within 0 ≤ R ≤ 1. At R = 1, we have a functional linear model when the factors fully describe the variance of the response function, as a result of which the residuals are zero (i = 0). At R = 0, the variability of the response function is completely determined by the residuals of i. [3]. It should be noted that in many PPSP, simultaneously with the value of R, an adjusted multiple correlation coefficient R_sk is also given, which makes it possible to eliminate the positive bias of the correlation coefficient.

$r_{CK}=\sqrt{1-\frac{D_{\epsilon }(n-1)}{D_y(n-m)}}=\sqrt{1-\frac{(1-r^2)(n-1)}{n-m}}\text{ (10)}$

where D_ε, D_y are sample estimates of the variance of the residuals and the response function, respectively. The difference R–R_sk is a correction for a positive displacement of the value R.

2. The linear coefficient of determination, which is the square of the multiple correlation coefficient

R₂ = D_y(x) /D_y = 1 – (D_ε/D_x) (11)

where D_y(x) is the variance of the response function values calculated using the regression equation; D_ε is the variance of the residuals. The coefficient of determination shows the proportion of the explained variance of the response function.

3. The standard deviation of the model:

${\sigma }_{y(x)}=\sqrt{{\displaystyle \sum {(y_i-{\tilde{y}}_i)}^2/(n-m-1)}}\text{ (12)}$

This value is functionally related to the linear coefficient of determination by the formula:

${\sigma }_{y(x)}=\sqrt{1-r^2}\text{ (13)}$

4. Standard errors of multiple correlation coefficient and regression coefficients:

${\sigma }_R=\frac{1-r^2}{\sqrt{n-m-1}}\text{ (14)}$

${\sigma }_{bj}=\frac{{\sigma }_y}{{\sigma }_{xj}}\sqrt{\frac{(1-r^2)D_{yj}}{(n-m-1)D_{yy}}}\text{ (15)}$

where σ_xj is the standard deviation of the predictor x_j; D_yj is the minor of the main determinant (determinant) for which the first row (y) and the jth column are crossed out; D_yy is the minor for which the first row and the first column are crossed out.

The use of formula (14) is legitimate in cases where the sample values of R obey the normal law, i.e. with relatively small values of R and a large length of the initial series n. For large values of R and small values of n, the Fisher z-transform should be used.

To check the parameters R and b_j for significance, a null hypothesis of the form H₀: R = 0, H0: b_j = 0 is formulated. The verification of this hypothesis is also carried out using the t-test:

R >t_ασ_R, , |bj| >t_ασ_bj.

If this condition is fulfilled, then the null hypothesis is rejected as untenable and the sample estimates of R and b_j are considered significant, i.e. deviating from zero in a non-random way. In most PPSP, the procedure for checking b_j values for significance is implemented through the p-criterion (p-level), which represents the level of significance that corresponds to the Student’s t-criterion, taking into account the number of degrees of freedom.

If this condition is fulfilled, then the null hypothesis is rejected as untenable and the sample estimates of R and b_j are considered significant, i.e. deviating from zero in a non-random way. In most PPSP, the procedure for checking b_j values for significance is implemented through the p-criterion (p-level), which represents the level of significance that corresponds to the Student’s t-criterion, taking into account the number of degrees of freedom.

5. The Fisher criterion used to assess the adequacy of the entire MLR model. For this purpose, the null hypothesis of the form H₀: _Dy(x) = D_ε is tested, i.e. the variance of the values of the response function calculated by the MLR equation is equal to the variance of the residuals. The null hypothesis is tested using the Fisher criterion:

F = D_y(x)(n – m – 1)/(D_εm) (16)

The calculated value of the Fisher criterion and compared with the table (critical) value F_кр((α, ν₁, ν₂) at a given significance level α and degrees of freedom ν₁ = m, ν₂ = n – 1. If inequality F > Fкр, the null hypothesis about the equality of the variances of the calculated values of the response functions and the residue is rejected and it is assumed that the variance described by the MLR model, non-random way different from that of the error variance. This means that the model under consideration is adequate, i.e. it corresponds well to the initial data of the response function. The reverse conclusion is made if F < F_кр.

The task of selecting effective predictors is directly related to the problem of constructing an optimal MLR model and in most modern PPMS packages is carried out simultaneously. The most effective method is the step-wise regression method. There are two most commonly used algorithms [7]: the inclusion method and the exclusion method.

The essence of the variable inclusion method is that at the beginning, at the first step, the predictor most correlated with the response function is selected and all parameters of the paired regression model are calculated. After that, based on the partial correlation coefficients, which show the “net” contribution of each variable to the variance of the response function, the subsequent variables with the maximum partial correlation coefficient are selected in turn. This procedure is repeated until all m models are built or the criterion is stopped.

The variable exclusion method implements the reverse procedure. First, a complete (from m variables) MLR model is constructed. Then the least significant factors are excluded from it in turn. This continues until the only significant factor remains. Note that if we compare the results of calculations using both methods, then even for the same set of variables there will be no complete identity. This is primarily due to the formal aspects. In the statistical literature [8,9], preference is more often given to the second method, since it provides an opportunity to consider all variants of models. However, with a large number of variables, the advantages of the first method include the absence of the need to build a complete MLR model. In this study, it is the method of including variables that is used.

When choosing the number of predictors of the regression equation that “best” describes the initial sample, unfortunately, there is no single correct method. In most PPSP, the standard procedure for stopping the calculation is based on setting the permissible minimum of F-inclusion and maximum of F-deletion, where the minimum of F-inclusion is F_in= F^a₁ (1,u-1), the maximum of F-deletion is F_out = F^a₁ (1,υ) for the significance level a and the number of degrees of freedom v. However, according to [1], such a choice of F values is not quite correct. The value of F can also be set by the researcher himself.

The process of including subsequent predictors in the regression model occurs after comparing the value of the F-variables with the value of the allowable minimum Fin, that is, the condition must be met: F > F_in. Similarly, variables are excluded. Thus, the set of predictors is determined when the calculated values of F cease to meet the specified criteria.

However, despite the fact that step-by-step algorithms are well developed, the use of this method involves making subjective decisions related to the choice of the optimal model. Obviously, finding the optimal MLR model is an informal task, and the more complex the initial model is, the more informal participation of the researcher is required to assess its optimal form [1]. On the one hand, if we want to obtain reliable forecasts using the selected model, then the largest possible number of variables should be included in the model. On the other hand, bearing in mind informal criteria (cost of information, availability, etc.), it is desirable to include as few predictors as possible in the equation. In addition, with an increase in the number of variables included in the regression model, a significant contradiction occurs: with constant sample size, the quality of the description of the response function increases, but the accuracy of all model parameters deteriorates [10,11].

The optimal model is a suitable compromise between these two extremes. Since there is no single statistical procedure, it is possible to use only a general scheme for evaluating the optimality of the model [1]. First of all, it is necessary to calculate the full range of models (from 1 to m), analyzing using different step-by-step algorithms and ranking predictors in different ways. After that, it is necessary to conduct a comprehensive analysis of the main parameters of the models (coefficient of determination, standard error of the model, Fisher’s criterion, p-level of regression coefficients). You should also take into account the fact that the simpler the model, the more reliable it is, so in cases where you have to choose from several models, you should always prefer a simpler one. As a result of a comprehensive analysis, it is possible to form an objective idea of the degree of reliability of the regression model, however, the task of choosing the optimal MLR model does not always have an unambiguous solution.

Factor analysis

In a narrow sense, factor analysis is understood as the method for identifying hypothetical (unobservable) factors designed to explain the correlation matrix R of quantitative observable features. It is assumed that the observed variables are a linear combination of factors. A factor is understood to be a hypothetical, not directly measurable, hidden (latent) variable in one way or another related to the original observed variables. The purpose of factor analysis is to identify hypothetical quantities among a large number of observed variables that are meaningfully interpreted and explain the totality of the studied variables as simply as possible.

The theoretical foundations of FA were laid in the 1930s and 40s by the American psychologist and mathematician Thurston [12]. He gave not only a general computational scheme but also proposed many constructive ideas, the development of which continues to the present time. In particular, Thurstone proved the basic factor theorem, proposed a centroid method for determining factors, a methodology for assessing generality, and formed the principle of a simple structure and ways to simplify factors.

If the principal component method (MGK) is considered a mathematical method that does not explicitly require preliminary statistical hypotheses, then factor analysis (FA) is already initially a statistical method. Its basic formula in matrix form is written as follows:

X = F.A′ + E (17)

where F is a matrix of values of common factors of size k×n; A’ is a matrix of coefficients of coupling of common factors and initial variables of size k×n, called factor loads; E is a matrix of residuals or characteristic factors (k×n).

The conditions imposed on the factor model (17) are as follows:

the common factors should be mutually independent;

common factors should be normalized and reduced to a single length;

common factors should not be correlated with errors;

errors should not be correlated with each other;

The number of common factors should not exceed half of the number of observed variables, i.e. k≤ m/2.

Calculation of common factors. The methods of factor analysis are usually divided into two groups: simplified and modern approximating [13]. Currently, the methods of the second group are mainly used, which assume that the first, approximate solution has already been found and is optimized in some way by subsequent steps. The maximum likelihood method is considered to be the most accurate and at the same time the most difficult [14,15]. However, the method of the main factors, which is included in most modern PPSP, has become the most widespread. It is based on the MGK, which allows you to obtain the initial factor loads in the m-dimensional feature space. After that, the transition from the m-dimensional space to the k-dimensional space of common factors is carried out, as a result of which those axes along which the observed variability does not go beyond the accepted errors are removed.

Then the secondary rotation of the axes is carried out already in the space of k common factors in such a way that as many factor loads as possible turn out to be close to zero, and the remaining factor loads, on the contrary, would be as close as possible to ± 1. This procedure is called the principle of simple structure. As a result, the variance of observations is redistributed and at the same time, the geometric structure of the source data is distorted. In cases where the best interpretability of the results is achieved, the use of MFAs can be considered justified.

Thus, the general block diagram for calculating common factors can be presented as follows (Figure 1).

X is a matrix of initial data of size mхn;

Z is a standardized matrix of the same size;

R is a correlation matrix of size mхm;

R^h is a reduced correlation matrix of size mхm;

λ is a vector column of eigenvalues of the matrix Rh with length m;

A₀ is a matrix of initial factor loads of size mхm;

λ^k is a vector column of eigenvalues of the matrix Rh of length k;

A is the matrix of final factor loads of size kхm;

F is the matrix of main factors of size kхn.

The first difference between MFA and MGK begins from the moment of transition from the usual correlation matrix to the reduced one, in which there are commonalities on the main diagonal instead of units. Recall that generality is a fraction of the variance of variables that can be explained through common factors.

In general, the magnitude of the generality can be written as h² = 1 – u², where u² is the variance of the characteristic. To determine the generality, several methods are used: the method of the greatest correlation, the Barth method, the triad method, the small centroid method, and the method of the square of the multiple correlation coefficient [13,15,16]. Most often, by default, the PPSP uses the latter method, according to which the value R2 is calculated for each variable with all other variables and substituted for the main diagonal instead of one.

Another important difference between the MFA and the CIM is the implementation of a procedure for the secondary rotation of common factors to improve their interpretability. In accordance with the principle of a simple structure, its main task, which consists of assessing the sufficiency of the number of turns, is usually solved on the basis of special criteria based on the representation of the variance of factor loads as a measure of the complexity of the structure of factors. This variance is calculated using the formula:

$D(F)=\frac{1}{k}{\displaystyle \sum _{q=1}^k(a_{jq}^2}-\overline{a_{jq}^2}{)}^2\text{ (18)}$

where a²_jq are the elements of the factor mapping matrix, i.e. the magnitude of factor loads, and k is the number of common factors.

It follows from formula (18) that the value of the variance will be maximum when one of the values of the squared loads is equal to the community h²_j, and all other elements in the line are zero. It is precisely in maximizing the criterion (18) by rotating the coordinate axes that the essence of the orthogonal rotation of the factor space consists. For this purpose, the following criteria are used [13,16]: quartimax, varimax, oblimax, quartimin, oblimin.

of these criteria, varimax, proposed by Kaiser, has been the most widely used, which best corresponds to the principle of a simple structure and has the form.

$V_r=\frac{m{\displaystyle \sum _{j=1}^m{a}_{jr}^4}-{\left({\displaystyle \sum _{j=1}^m{a}_{jr}^2}\right)}^2}{m^2}\text{ (19)}$

The values of aij obtained as a result of such orthogonal rotation are accepted as the final factor loads. Note that in cases where, according to the researcher, orthogonal rotation does not lead to achieving the “necessary” results, oblique rotation procedures (oblimax, quartimin, oblimin) can be used, in which the factors become correlated with each other. Obviously, this contradicts the classical formulation of the MFA problem and significantly expands the initial set of its assumptions.

In addition, non-orthogonal rotation introduces an element of subjectivity into the already rather arbitrary rotation of the task, which is advisable for everyone to avoid, excluding experts. We also emphasize that secondary rotation distorts the geometric structure of objects in the factorial space. This can lead to both an improvement and a deterioration in the physical interpretability of the source objects.

Results

The main patterns of formation of biological and commercial productivity of the waters of the South China Sea

Features of tuna distribution in the World Ocean: Tuna includes about forty species found in tropical, subtropical, and temperate latitudes of the World Ocean. The main tuna populations are distributed from 40°c to 40 ° C, although shoals of tuna are found in higher latitudes during the warmer months. According to the Food and Agriculture Organization (FAO), if the global tuna catch in 1950 was less than 1 million tons, then by 2009 it reached 6.5 million tons, i.e. it increased at a rate of about 0.1 million tons/year. At the same time, striped (40%) and yellowfin (18%) tuna make up the basis of the global catch.

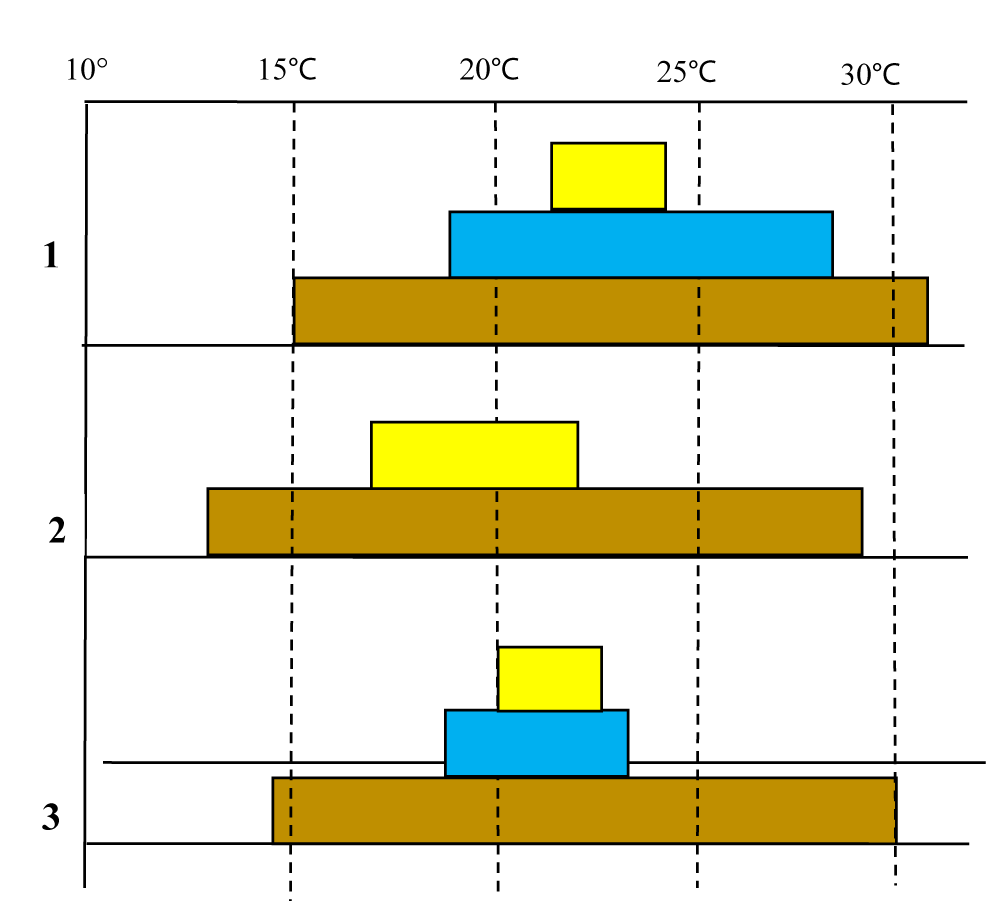
Tuna live at different depths: large tunas up to depths of 300-400 m, the vertical distribution of small tunas is limited to depths up to 100 m, although they are most often found in the uppermost layer of water up to 50 m. Tuna usually migrates at a speed of 9-10 knots, sometimes up to 15-18 knots. The mass of large tunas is usually several tens of kilograms, the length is more than 1 m; the mass and length of small tunas are 3-5 kg and 50-60 cm, respectively. It is very important that tunas react very sensitively to changes in water temperature, and for each of their species there is an optimal temperature regime of habitat (Figure 2). Similarly, tunas react to changes in salinity and the transparency of the water. The optimal salinity of the water for them is 35.5 %, and the transparency is 25-30 m [17-21].

Features of tuna distribution in the waters of the South China Sea

In the South China Sea, tuna distribution can be divided into two zones according to the nature of monsoon activity. During the northeast monsoon, when fishing takes place from October to March, tuna is distributed mainly in the northern part of the South China Sea and near the Paracel Islands (12o00 N - 17o00 N and from 110o00 E - 115o30E). During the southwest monsoon (from April to September), tuna is distributed in the southern part of the South China Sea and off Spratly Island (6o00 N - 11o30 N and from 108o00 E - 114o00 E).

Figure 3 shows the distribution of the main tuna fishing areas by Vietnamese vessels. The fishing area I (Hoangsa) represents the northern part of the South China Sea, fishing areas II, III, IV, and V represent the central areas of the sea of Vietnam and area VI represents the southern zone off the coast of the sea of Vietnam. The maximum catch is observed in September, which is 12.5% of the average annual catch. The least amount of fish is harvested in November-December (about 7.3%), i.e. intra-annual differences in fish catch are small.

The influence of water temperature on the biological productivity of the South China Sea

As is known, out of a large number of abiotic factors, the water temperature has the greatest influence on biological productivity, the effect of which on the vital activity of marine organisms is extremely multifaceted. The long-term experimental studies carried out in Vietnam on various characteristics of water temperature and parameters of bioproductivity of seawaters allow us to assess the degree of interrelation between them. Of the 26 indicators, 18 represent different temperature characteristics. and 8 are the parameters of bioproductivity. Table 1 shows the sample coefficients correlations between them for the period 1990-2009. Previously, we noted that all the characteristics of bioproductivity are closely related to each other, the correlation between them does not fall below r = 0.85 [22-25].

As can be seen from Table 1, the maximum correlation of all bioproductivity parameters is noted for the isotherm depth of 24 OC (r=|0,70-0,94|). The second most important is the depth of the isotherm of 20 oC. A significant correlation at the level of α=0.05 (gcr=0.42) is also observed with the thickness of the upper homogeneous layer of water and the temperature of the sea surface. With all these parameters, the correlation turns out to be negative. This means that with the deepening of isotherms 20 and 24 oC, an increase in the thickness of the quasi-homogeneous layer, and an increase in sea surface temperature, all the characteristics of bioproductivity should decrease. At the same time, the characteristics of bioproductivity react poorly to the variability of the layer thickness between isotherms 20 and 24 OC (r=|0,20-0,52|). It should also be noted that the temperature range of 20-24 oC is optimal for the distribution of tuna.

So, it is quite obvious that the significant influence of various characteristics of water temperature on all parameters of the biological productivity of the South China Sea, of which the most important should be considered the depth of the isotherm of 24 OC.

The spatiotemporal variability of the isotherm depth is 24 oC

First of all, let’s consider the average annual (1980-2008) distribution of the isotherm depth of 24 oC according to CARTON-GIESE SODA data (Figures 4,5). It is easy to see that H₂₄ gradually increases from 51 m in the extreme northwest of the district to 76-78 m in its southern part at latitude 9o S. Further south, H₂₄ begins to decrease. A much more complex character is characteristic of seasonal changes in the average annual monthly values of H₂₄, however, for most points the annual course of H₂₄ is practically absent and the distribution of H₂₄ is mainly random, which is due to the fact that the maximum and minimum values of H₂₄ can occur in any season of the year. The absolute maximum of H₂₄ is observed in January at point 17 (101.4 m), and the absolute minimum is in June at point 1 (33.2 m).

Given the relatively short length of the H₂₄ time series (n=29), the calculation of cyclic fluctuations is impractical, therefore, only linear trends were calculated for all points of the selected water area. The spatial distribution of the angular trend coefficients (Tr) is shown in Figure 5. As can be seen, trends in the entire sea area are positive, i.e. there is a tendency to deepen the isotherm of 24 oC. The maximum trend values are confined to the shallow northwestern part of the district. At the same time, significant trends, i.e. deviating from zero in a non-random way, are peculiar to the value Tr ≥0.35. The presence of positive trends means that during the period under review, there was a tendency to decrease the bioproductivity of sea waters.

In order to study the spatiotemporal structure in more detail, the matrix of average annual values of H₂₄ with a size of 23x29 was subjected to classical factor analysis. The analysis of the eigenvalues showed that it is possible to limit ourselves to the first five factors, which describe 78% of the variance of the initial field. Table 2 shows the contribution of individual eigenvalues (factors) to the dispersion of the H₂₄ field after the second orthogonal rotation by the varimax Kaiser method, which partially redistributed the variance between the factors. As a result, the fourth factor became the second, and the third – the fifth. That is why there are not very significant differences between the factors.

The results of the zoning of the KM water area according to the interannual fluctuations of H₂₄ are shown in Figure 6. The district number corresponds to the factor number (proper number). As expected, the largest area is occupied by the first district, which is characterized by the highest interannual variability of H₂₄ values. The smallest fifth district serves as a buffer zone between the first and fourth districts.

A statistical model of tuna catch based on the water temperature of the surface layer of the sea

The temperature of the sea surface layer (TPM) is one of the important factors affecting the bioproductivity and distribution of tuna [21,23,25]. On average, during the year, the TPM in the South China Sea varies in the range of 26-29 oC (Table 3).

In order to study the impact of TPM on tuna fishing, a time series of average annual TPM values was formed at 23 points in the South China Sea for the period 2000-2014, corresponding to the data of the total annual tuna catch by Vietnamese trawlers. So, the original model looked like:

V = f (bj ;TPM_0j), where j = 1...m (m=23) (20)

Unknown coefficients bj were determined by the method of including variables in the step-by-step procedure of the multiple linear regression model (MLR). The optimal model for catching tuna at the fifth step (Table. 4) has a high coefficient of determination (R2=0.86), a small standard error (6743 tons or 13%), and significant Fisher and Student criteria (p-level). Naturally, there is a very good correspondence between the actual and calculated values of fish catch using the MLR model.

The current state of tuna production

The South China Sea is a very important fishing area, where 10 countries closest to the sea are fishing, and it is extremely important for the development of the economy and the provision of seafood to the Vietnamese population. In recent decades, there has been a fairly rapid increase in the population of Vietnam and a significant growth in the country’s economy. Over the period 2000-2014, the population increased by about 15%, and the gross domestic product increased 6 times! In terms of economic growth, Vietnam is one of the leaders in Southeast Asia. Naturally, such rapid economic growth in Vietnam has made it possible to increase the fishing fleet and its capacities almost annually. Thus, the number of fishing vessels increased more than 3 times during the period under review, and their total capacity increased more than 4 times!

During the period under review (2000-2014), the total annual tuna catch by Vietnamese vessels increased by more than 2 times and reached 80,000 tons in 2014 (Figure 7). At the same time, tuna fishing by Vietnamese vessels in the South China Sea is conducted in four main ways (as a% of its total catch): these are gill nets (50%), purse seine (29%), fishing rod and longline (21) fishing. A comparative analysis of the catch of various tuna species shows that the largest share of the total catch for the period 2000-2014 was for striped tuna (61%). Yellowfin tuna is in second place (31%), and bigeye tuna is the least produced (7%). Other tuna species do not have commercial stocks in the South China Sea.

Statistical model of tuna catch depending on economic and oceanological factors

The number of fishing vessels, their total capacity, gross domestic product (GDP), and the population of Vietnam were considered as economic factors in this work. To assess the degree of their connectivity with fishing, the nonparametric Spearman correlation coefficient was used (Table 5).

From the Table 5 It can be seen that there is a high correlation between all factors, which is mainly due to the presence of well-defined trends in the time series. All correlation coefficients are significant according to the Student’s criterion (at α =0.05 g_cr = 0.50). Tuna catch has a minimal correlation with the population (r=0.81) and a maximum correlation with the number of fishing vessels (r=0.87). It follows that tuna fishing (V) is largely determined by economic reasons, while the role of oceanological conditions in tuna fishing is secondary. Using the least squares method, a regression model was calculated with the number of fishing vessels N:

V = V_ec + V_oc = 7495 +1.964N + δV (21)

where δV are the remnants of the model, which are determined by oceanological conditions. This equation and its coefficients are significant according to the criteria of Fisher and Student, the coefficient of determination is R2 =0.75, and the average square error σ = 7497 t/year, which is 15% of the average catch value. The next task is to build a model for the δV component, in which the TPM anomalies selected from the NOAA NCDC ERST archive were taken as the initial variables. To build a model in the form:

δV = f(bj ;DTMJ), (22)

where bj are unknown coefficients to be determined, the method of including variables of the stepwise algorithm of the multiple linear regression model was used. After that, a detailed analysis of the main parameters of the models (coefficient of determination, standard error of the model, Fisher criterion, p-level of regression coefficients) was carried out for significance at each step. Up to and including step 8, the model parameters were significant, however, starting from step 9, regression coefficients appeared in the model, insignificant according to the Student’s criterion. Thus, an equation with 8 variables of water temperature anomalies was adopted as the optimal model:

δV = b₀ + b₁ΔTPM₁ + ... + b₈ΔTPM₈, (23)

which describes 95% of the variance of the δV series, has a small standard error of tuna catch (σ = 2514 tons/year), a significant Fisher criterion for the model, and significant Student criteria for all variables. As a result, in general, the statistical model of tuna catch in the South China Sea has the form:

V = a₀ + a₁N + ${\displaystyle \sum _{i=0}^8{b}_i}$ ∆TPMi (24)

This model describes 98% of the variance of the initial time series of tuna catch, and the random catch error according to the model is 1590 tons/year, i.e. 3%.

Methodological aspects of fish catch forecasting

The problem of long-term prediction of tuna catch seems to be very difficult for the very reason that for short time series, it is impossible to investigate and identify the inherent internal patterns of variability and frequency structure. In principle, in relation to the problem under consideration, it is advisable to divide forecasting methods into 3 groups: expert, extrapolation, and statistical methods. Given the short length of the time series of fish catch and the fact that the linear trend describes the predominant proportion of its variance, the most acceptable option for developing a long-term forecast of tuna catch is extrapolation methods. Forecasting tuna catch in the South China Sea. For the first time, a method for long-term forecasting of annual tuna catch values based on extrapolation of a time series with its approximation by a polynomial model and a second-order autoregressive model is proposed. Due to the short length of the fish catch time series and the fact that the trend describes the predominant proportion of its variance, this approach seems to be the only possible one. Two numerical procedures are implemented in the work. The first was to isolate a linear trend and approximate the residuals obtained after its elimination by a polynomial model. The calculated linear trend equation has the form:

V = a₀ + a₁t + δV* (25)

where t is the time, δV* is the residuals. Equation (6) describes 65% of the variance of the initial series and has a standard error equal t_o σ=8288 t/year. The use of the “Approximation” software package has shown that the most accurate way to approximate the residues of δV* is a polynomial of degree 5, i.e.

δV* = b₀ + b₁t + b₁t₂ +… + b₅t⁵ (26)

The coefficient of determination of this dependence is R2=0.84, and the standard error is σ=4236 t/year. Now summing up the components in formulas (6) and (7), we get a fish catch that functionally depends only on time:

V = a₀ + b₀ + (a₁+ b₁)t + b₁t² +… + b₅t⁵, (27)

This equation describes 95% of the variance of the initial series and has a standard error equal to σ=3250 t/year, which is 5% of the average value. Another option for constructing an extrapolation model is to use an autoregressive model in relation to residues in formula (6) of the form:

H^o(t) = a1Xo(t-1) + a₂X^o(t-2) + ... + α_рX^о(t-p) + Z(t), (28)

where X^o(t) is a centered random process, Z(t) is white noise. To estimate the order of the autoregression model, we use a private autocorrelation function (CHAKF). At the first shift, τ=1, the partial autocorrelation coefficient coincides with the usual autocorrelation coefficient, i.e. r _part(t₁) = r(τ₁). At the second shift τ=2, it takes into account the influence of r(t1) on it. Figure 8 shows a graph of the CHAKF, from which it can be seen that in the first two shifts, there is a high partial correlation exceeding the critical value of the correlation coefficient at the significance level α = 0.05 (r_cr = 0.50). However, at subsequent shifts of τ≥3, it decreases sharply and becomes insignificant. It follows that, in principle, we can use first- and second-order autoregression models, i.e. p=1 and p=2.

Having calculated the autoregression coefficients using the Yule-Walker method, it is not difficult after that to calculate the values of δV * using formula (9), adding which with the trend component we obtain estimates of tuna catch.

The forecast for the linear trend (6) for 1 step (for 2015) gives an estimate of fish catch equal to 72100 tons/year, and according to equation (8) – 82,000 tons/year, which almost coincides with the actual catch of fish in 2014. The forecast using the autoregression model of the first and second order gives an estimate of tuna catch for 2015 equal to 81,500 and 77,200 tons/year, respectively. It can be seen from this that the second-order autoregression model significantly underestimates the estimate of fish catch. However, only a comparison with the actual catch can determine which forecast estimates are more accurate. After this work was completed, an estimate of the tuna catch by Vietnamese vessels for 2015 was obtained. It amounted to 78.670 tons, i.e. it almost coincides with the prognostic estimate based on the second-order autoregression model. As for the forecast of tuna catch for 2016, if we focus on extrapolation models, it may decrease.

Discussion

As a result of the research carried out in the work, the following main conclusions were drawn.

1. The commercial stock of tuna according to the Scientific Research Institute of Marine Fisheries of Vietnam is estimated at 662-670 thousand tons. At the same time, the total allowable catch is about 233 thousand tons, and currently, about 80 thousand tons per year are mined. In the South China Sea, tuna distribution can be divided into two zones according to the nature of monsoon activity. During the northeast monsoon, when fishing takes place from October to March, tuna is distributed mainly in the northern part of the South China Sea and near the Paracel Islands. During the southwest monsoon (from April to September), tuna is distributed in the southern part of the South China Sea and off Spratly Island. The maximum catch is celebrated in September. The least amount of fish is harvested in November-December. Striped tuna accounted for the largest share of the total catch in the period 2000-2014 (61%). Yellowfin tuna is in second place (31%), and bigeye tuna is the least produced (7%). Other tuna species do not have commercial stocks in the South China Sea. Most tuna is harvested using gill nets (50%), purse–line fishing provides 29% of the total catch, and longline and fishing line fishing - another 21%.
2. The assessment of the influence of 18 different water temperature indicators on a complex of 6 parameters of the bioproductivity of the waters of the South China Sea for the period 1990-2009, which are closely related to each other, the correlation between them does not fall below r= 0.85. It is shown that the maximum correlation of all bioproductivity parameters is noted for the isotherm depth of 24 oC and ranges from r=-0.70 to r=-0.94. The second most important is the depth of the isotherm of 20 °C, and the third is the temperature of the sea surface. With all these parameters, the correlation turns out to be negative. This means that with the deepening of isotherms 20 and 24 oC and an increase in sea surface temperature, all the characteristics of bioproductivity should decrease. At the same time, although the range of 20-24 oC is optimal in the distribution of tuna, the characteristics of bioproductivity react poorly to the variability of the layer thickness between isotherms 20 and 24 oC.
3. A detailed analysis of the spatial and temporal patterns of the depth of the isotherm 24 oC (H₂₄) was performed on the basis of the deep-sea archive of CARTON-GIESE SODA for the period 1980-2008. In particular, there is a significant spatial differentiation of H₂₄ values, both in the zonal and meridional directions. For average long-term annual conditions, the values of H₂₄ gradually increase from 51 m in the extreme north-west of the district to 76-78 m in its southern part at latitude 9o S. Further south, H₂₄ begins to decrease. There is also an increase in H₂₄ values from coastal areas to the open sea. The calculation of linear trends showed that positive trends are observed in the entire sea area, i.e. there is a tendency to deepen the isotherm of 24 oC. The maximum trend values are confined to the shallow northwestern part of the district. The presence of positive trends means that during the period under review, there was a tendency to decrease the bioproductivity of sea waters.
4. For the first time, on the basis of factor analysis, the zoning of the South China Sea fishing area was performed according to the nature of interannual fluctuations of the isotherm of 24 oC. The first 5 factors describe almost 80% of the variance of the initial field. According to factor loads, 5 quasi-homogeneous regions were identified. The largest area with the maximum interannual variability of H₂₄ is stretched in a meridional direction along the coast of Vietnam. The rest of the districts have a latitudinal orientation. Mainly random interannual fluctuations are observed in the time course of common factors. One can only note the presence of a weak 6- to 8-year cycle, which is also manifested in tuna stocks in the world’s oceans.
5. For the first time, a statistical model of the interannual values of tuna catch was constructed depending on economic and thermal factors. It is shown that the most important economic factor is the number of fishing vessels, which increased by more than 3 times over the period 2000-2014, and their total capacity by more than 4 times! The thermal factor was the sea surface temperature (TPM) in the nodes of the two-degree grid, which is determined with high accuracy, is available almost online, and has a significant correlation with both the characteristics of bioproductivity and H₂₄. It is shown that the economic factor (the number of fishing vessels) is the main one, accounting for 75% of the variance of the initial series. The remnants from this model served as the initial data for constructing a regression model with TPM anomalies, taken from the well-known NOAA NCDC ERSSTv4 archive. An optimal model containing 8 variables is obtained, which describes 95% of the variance of the residual series with a significant Fisher criterion for the model and a significant Student criterion for all variables. As a result, the general statistical model of tuna catch, depending on the number of vessels and TPM, describes 98% of the variance of the initial series, and the random error of catch according to the model is 1590 tons/year, i.e. 3%.
6. For the first time, a method for long-term forecasting of annual tuna catch values based on extrapolation of a time series with its approximation by a polynomial model and a second-order autoregressive model has been proposed. Due to the short length of the fish catch time series and the fact that the trend describes the predominant proportion of its variance, this approach seems to be the only possible one. Two numerical procedures are implemented in the work. The first consisted in approximating the residues obtained after excluding the linear trend from the time series of tuna catch by a polynomial of degree 5, which describes 95% of its variance and has a standard error equal to s=3250 t/year, i.e. 5% of the average value. The second approach was to use an autoregressive model for the same residues, which is a stationary random process. As a result of calculating the partial autocorrelation function, it was found that the second-order model is optimal. The independent forecast of tuna catch for 2015 according to the polynomial model gave a value of 82,000 tons/year, and according to the autoregressive model – 77200 tons/year. After making a forecast from Vietnam, it was obtained that the actual tuna catch in 2015 amounted to 78,670 tons/year. The discrepancy with the first model is 4%, with the second – less than 2%.

Conclusion

The South China Sea is characterized by exceptionally high biological productivity of its waters, which contributes to the formation of large commercial stocks of pelagic fish. Of particular importance is the tuna fishery, as it is extremely valuable in terms of food and enjoys unlimited demand among consumers. Tuna fishing ranks first in the structure of Vietnam’s exports of marine fish products to more than 60 countries around the world, and in 2015 it amounted to more than 408 million US dollars. The government of the country set a strategic goal of sharply increasing the fishery by accelerating the construction of new, more powerful fishing vessels, reorganizing the coastal infrastructure, using new technologies in processing fish products, and expanding cooperation with other countries in the region and the world. The purpose of this work is to identify the impact of various oceanographic characteristics on the parameters of the bioproductivity of the waters of the South China Sea, build an effective statistical model of tuna catch depending on oceanographic and economic factors, and develop a method for long-term forecasting of tuna catch.

1. Malinin VN. Statistical methods for analyzing hydrometeorological information. St. Petersburg: Publ. RSHU. 2008;325.
2. Anderson T. Statistical analysis of time series. Moscow, Mir. 1976;755.
3. Anderson T. Introduction to multivariate statistical analysis. Translation from English. Moscow: Fizmatgiz. 1963;499.
4. Kosolapkin GY, Fortus VM. On the relationship between the optical and hydrological structure of the waters of the South China Sea in the winter season. Vladivostok, Publ. TOO DVNC USSR Academy of Sciences. 1987;14.
5. Melnikov VN. Biotechnical foundations of industrial fisheries. Moscow. 1983;189-199.
6. Melnikov AV, Melnikov VN. Commercial Fish Stock Management and Nature Conservation. Astrakhan. 2010;14-19.
7. Afifi A, Eisen S. Statistical Analysis: A Computer-Based Approach. Moscow, Mir. 1982;488. Available from: https://www.academia.edu/93768562/Statistical_Analysis_A_Computer_Oriented_Approach
8. Vainovsky PA, Malinin VN. Methods of Processing and Analyzing Oceanographic Information. Part 2. Multivariate Analysis. St. Petersburg: Publishing House of the Russian State Medical Institute. 1992;96.
9. Draper N, Smith G. Applied Regression Analysis. Book 1, 2. Moscow: Finance and Statistics. 1986;366.1987;351.
10. Smirnov NP, Vainovsky PA, Titov YE. Statistical diagnosis and forecast of oceanographic processes. St. Petersburg: Gidrometeoizdat. 1992;198.
11. Malinin VN. Ocean level: present and future. St. Petersburg: RSHU. 2012;260.
12. Thurstone LL. Multiple factor analysis. Univ. Chicago Press, Chicago. 1974;535. Available from: http://www.stats.org.uk/factor-analysis/Thurstone1931.pdf
13. Tamashevich VN. Multivariate statistical analysis in economics / Ed. Moscow: UNITY-DANA. 1999;598.
14. Iberla K. Factor analysis. - Moscow, Statistics. 1980;398. Available from: https://www.scirp.org/reference/referencespapers?referenceid=807121
15. Harman G. Modern factor analysis. M. Statistics. 1972;486.
16. Blagush P. Factor analysis with generalizations. M. Finance and Statistics. 1989;247.
17. Belkin SI. Tuna fishery / S.I. Belkin, E.V. Kamensky. M. Food industry. 1976;26.
18. KienND. Assessment of the current state of world tuna stocks based on the materials of literary sources / Nguyen Dang Kien // Natural Sciences "Journal of Fundamental and Applied Research". Bulletin of the Astrakhan State University. Astrakhan. 2013;4(45):46-64.
19.  Kien ND, Bukharitsin PI. Investigation of the influence of some environmental factors on the distribution of pelagic fish in the South China Sea (on the example of tuna) / Nguyen Dang Kien, P.And Bukharitsin // Fisheries "Aquatic bioresources and their rational use". Bulletin of Astrakhan State Technical University. un-ta. Astrakhan: Publishing House of AGTU. 2014;2:13-20.
20. Kien ND, Bukharitsin PI. Biological features and habitat conditions of some tuna fish /Nguyen Dang Kien, P.I. Bukharitsin //Fisheries. Bulletin of Astrakhan State Technical University. un-ta. – Astrakhan: Publishing House of AGTU. 2015;1:134-140.
21.  Kien ND, Malinin VN, Gordeeva SM. The influence of water temperature on the formation of biological and commercial productivity of the South China Sea / Nguyen Dang Kien, V.N.Malinin, S.M. Gordeeva //Scientific notes of RSMU. 2016;42.
22. Kien ND, Malinin VN, Gordeeva SM. Statistical modeling of tuna catch in the South China Sea. / Nguyen Dang Kien, V.N.Malinin, S.M. Gordeeva //Scientific notes of RSMU. 2016;42.
23. Bukharitsin PI, Kien ND. The influence of water temperature on the state of the population and tuna fishery in the South China Sea. Prediction of tuna catch depending on oceanological and economic factors / ISBN:978-3-659-90966-5. Monograph. Werlag / Publisher: LAP LAMBTRT Academic Publishing. 2016;24c.
24. Arrizabalaga H, Dufour F, Kell L, Merino G, Ibaibarriaga L, Chust G, et al. Global habitat preferences of commercially valuable tuna. A deep-sea study. Part II: Case study. Oceanography.2015;113: 102-112. Available from: 10.1016/j.dsr2.2014.07.001
25. Wang H. A study on the biology and habitat distribution of bigeye tuna in the high seas of the Central and Western Pacific Ocean [D]. (Shanghai Ocean University). 2020. Available from: 10.27314/d.cnki.gsscu.2020.000610